 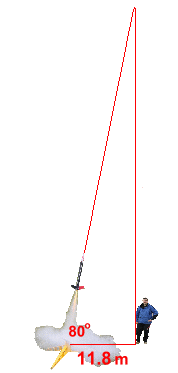
In order to calculate the height that one of our rockets reached, we examined the flight path of several rockets to see what they were doing. They were being launched at an angle slightly off vertical. We noticed that the rockets seemed to climb at a steep angle, following a fairly straight path, until the motor burned out, at which point the rocket began to drift. In order to calculate the height the rocket reached up to the point of burn-out, we needed to locate a position on the ground directly under the burn-out point. Mr. Phelps positioned himself at this location, and we measured the distance from the launching point to be about 11.8 metres. We also measured the angle that the rocket left the launch pad with a large protractor; this angle turned out to be about 80°. 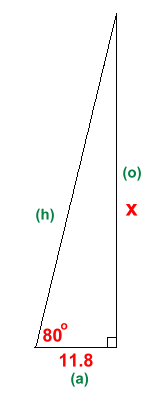
This gave us a right triangle. We know the bottom angle and the adjacent side. To calculate the height of the opposite side X, we will set up a trigonometric ratio, and then solve it for X: 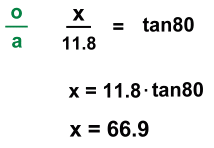 This works because the ratio of sides in an 80° right triangle is always the same, so a calculator knows what x/11.8 is supposed to be ... that's what tan80 is. The result shows that this particular rocket rose to a height of about 67 metres before the motor burned out.
|