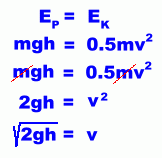This is the Sky Flyer. This ride is so terrifying, they actually charge you an extra $18 to go on it. (All the other rides are free with admission) People are lined up here all day! You can be by yourself, or with a group of three, tightly tied onto a little mat that is hoisted 45 metres into the air and allowed to drop. You swing, at almost 100 km/h near the bottom. Just over the heads of passersby. During the Spanish Inquisition they would have paid good money for a torture device this effective! Here's where it starts. You get tied onto a tiny mat, face down, that is suspended on the end of a long cable. Your head and feet stick out. This means that in a moment you will be looking straight down from a height of 45 metres, or almost 150 feet. Once you're buckled in at the end of that long cable, they'll begin hauling you upwards. Incidentally, this ride gets shut down immediately whenever there's a storm. It makes a good lightning rod. With you on the end. This is an image of several riders during the initial plunge, when the cable swings them down over the spectators' heads. At this point, according to the ride's description, they are moving at about 96 km/h. It's not a good idea to stand directly under their swing (they pass by about 10 feet over your head) since various wet fluids have been known to emanate from the vicinity of the mat ... The ride description also suggests that you not go on this ride if you are pregnant (O.K., I can understand that) or have a heart condition. It doesn't say what they will do if you end up with a heart condition. The ride acts like a giant pendulum, with you on the end. Here's the picture again, after the cables used to haul you into position have let go. The length of the pendulum cable L determines how long your swing will be. (This is called the period of the swing). The usual equation for relating the period T and length L of a pendulum, as studied in Physics 20, is: where g is the acceleration of gravity, 9.8 m/s2    We can't use this equation reliably here, because it only works for small angles of release. From the picture, you can see that the riders are pulled to a 90° angle ... too large to use this formula. We can however do a simple calculation to check the speed at the bottom. When the riders have been hoisted up to the left, their height above the ground is h. Their potential energy Ep due to height is given by the formula  Ep = mgh, where m is the total mass of them and the mat. At the bottom of the first swing, when they have essentially been in freefall, and are close to the ground, their height is close to zero, and almost all of their energy due to height has been transformed into kinetic energy of motion. Their kinetic energy Ek at this point is given by the formula  EK = 0.5mv2, where v is their speed. The original potential energy must be about equal to the kinetic energy it turned into. In other words, EP = EK. By equating the formulas, we can solve for an expression for speed. Here's the algebra: So a rough formula for the speed of a pendulum at the bottom of its swing is: where h is its height at the top of the swing. Here's the calculation using height 45 m: Our rough estimate gives an answer which is close to the posted value of 96 km/h. (Because the pendulum does not let you descend the full 45 m, you don't get quite as much kinetic energy, and of course, friction in the cable mechanism is causing you to lose some energy too). Amusement Park Physics