|
In a Triangle 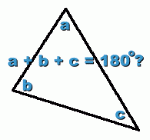 What do the three angles in a triangle add to? You may think you already know the answer to this question. The angles add to 180°, right? In fact, you only know part of the answer. The angles in a triangle only add to 180° sometimes! Under certain conditions they add to more than 180°, and sometimes less. Let's look at why. 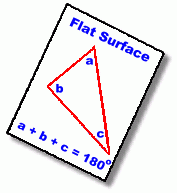 The situation with which you are familiar is the one where a triangle is drawn on a flat surface, called a plane. Such surfaces, like the page in your math notebook, are perfactly flat. They are described by saying they have zero curvature. Whenever you draw three straight lines to form a triangle here, the three angles formed will always add to exactly 180°. But there's no reason we have to draw the triangle on a flat surface ... 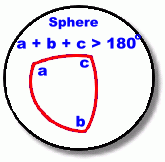 Suppose instead we draw the triangle on a sphere. Using a flexible ruler, we draw three straight lines on the surface of a sphere, and then measure the angles. We discover that the sum of those three angles is greater that 180°! This is not a trick. It's difficult to show on a page like this, so we urge you to get a globe or large ball, and draw three straight lines with a ruler, that connect. Measure the angles. You will find for yourself that the angle sum exceeds 180°. This is because a sphere has positive curvature. This is a very important fact. It means, for instance, that triangular paths drawn across the surface of the earth that are long enough to follow the curvature of the earth (which is very nearly a sphere) will total more than 180°. 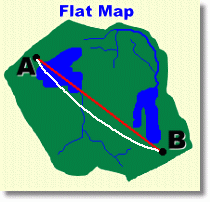 Another way of saying this is that the shortest distance between two points on earth is not a straight line on a map. On a flat map of a region of the earth, as shown on the right, you might assume that the shortest distance between points A and B is shown by the straight line joining them. If in fact the earth were flat, this would be true. But the earth's surface is not flat ... it is the curved surface of a sphere. The shortest distance is the arc (centred at the centre of the earth), shown in white. This is called a 'great circle', the path flown by airplanes to cover the least distance from A to B. 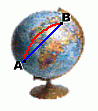 You can try this to convince yourself it's true. Get a flat map of a large region of the earth, and lay out a straight-line path between two points A and B. Identify some points in between that lie along the line.Now locate and mark points A and B and the in-between points on a large globe, and draw the same path. You will see that this path is longer than the path directly from A to B along the surface of the globe. If you locate points along that line on the globe, and transfer them back to the flat map, you will get a curve. Is there a condition uder which the angles in a triangle add to less than 180°? 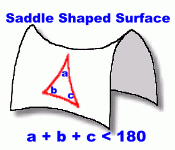 Yes there is. This will happen on a surface which has negative curvature. An example is the inner curve of a saddle-shaped surface, as shown on the right. Triangles drawn on this surface will have three angles that do indeed add to less than 180°!  This fact is important whenever shapes with negative curvature are constructed ... large stadium roofs, for example. |