 We will assume that you know how to find derivatives of various functions. We use the chain rule when differentiating a 'function of a function', like f(g(x)). It helps us differentiate 'composite functions' The chain rule states that the derivative of f(g(x)) is f'(g(x)) · g'(x). If y = f(g(x)), then y' = f'(g(x)) · g'(x). g is the function within f, so we call g the 'inner' function and f the 'outer' function. You differentiate the outer function while keeping the inner function the same, then multiply this by the derivative of the inner function. 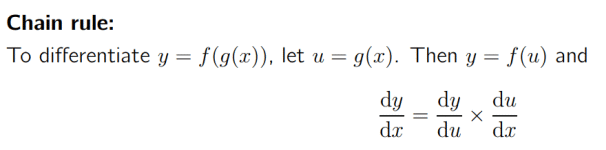
Let's do some examples. Example 1: What is the first derivative of y = (5x+6)2 y = (5x+6)2 If y = u2 then y' = 2u1 · (derivative of u) y' = 2(5x + 6)1 · (5) and simplify: y' = 10(5x + 6) y' = 50x + 60 Example 2: If y = (3x - 7)12, find y' y = (3x - 7)12 y' = 12(3x - 7)11 · 3 y' = 36(3x - 7)11 Example 3: Find the derivative of the function f(x) = (2x2+5)3 f'(x) = 3(2x + 5)2 · (4x) f'(x) = 12x·(2x + 5)2 Example 4: Differentiate: Change the radical to an exponent first: 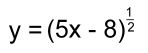 Now use the Chain Rule: 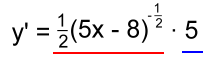 Finally, simplify and put back the radical: 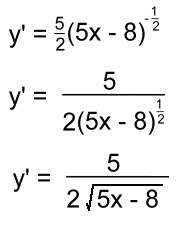
Example 5: Find the derivative of y = sin(3x2 + x) The derivative of sin is cos: y' = cos(3x2 + x) · (6x + 1) y' = (6x + 1) · cos(3x2 + x) Example 6: Differentiate y = cos(x2) The derivative of cos is -sin: y' = - sin(x2) · 2x y' = -2x·sin(x2) Example 7: 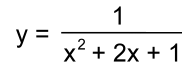 Replace the fraction by an exponent: 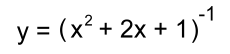 Use the Chain Rule: 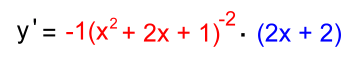 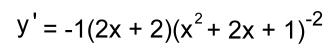 Ordinarily we would stop here. But we noticed something: 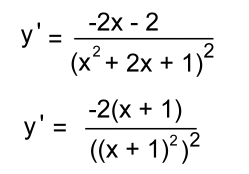 The top and bottom factor to give the same base (x + 1): allowing us to reduce the fraction: 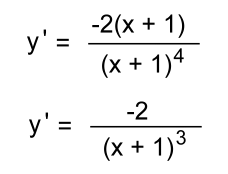
|