There is a fascinating relationship between the circumference of a circle and the slope of a line ... two topics which you might have thought were not related at all. Let's have a look.

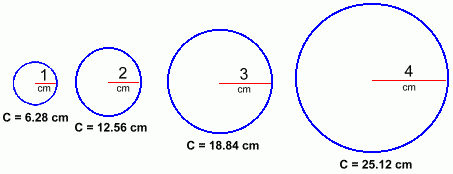
Here are four circles, with radii of 1 cm through 4 cm. The corresponding circumference of each circle has also been measured.

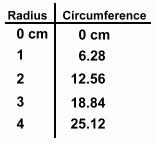Here are the same numbers in table form.
We started with a circle of zero radius, in order to make the table complete.

You can see that as the radius of a circle gets bigger, so does the circumference.
That's obvious, we hope.

Putting the data in table form suggests that we might make a graph of circumference versus radius:

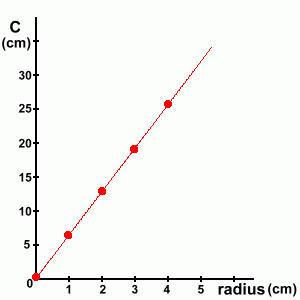Here's the graph, using the values for radius and circumference from the circles shown above.

The values we plotted clearly line up, so we connected them with a line. This indicates that there are many circles with radii in between these numbers that we could have plotted.

The relationship between circumference C and radius r is obviously a linear one. In other words, the graph forms a straight line, and the equation must look like:

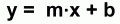
Can we find the equation of this line?
To do that, we'll need to find both the slope  m and the y intercept  b.

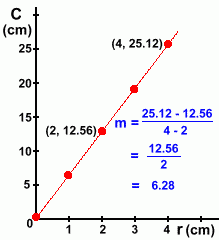Here is the graph again, with the work shown in evaluating the slope of the line.

The slope  m is  6.28

By looking at the graph, the y intercept can be determined easily:

The y intercept  b is  0

Now we can write the equation of this line ...

The equation must be of the form:

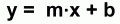
Since  m is 6.28 and b is  0, and we're relating  C to  r:


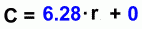
Now we can drop the zero, which gives us this equation for the line illustrating the relationship between circumference and radius:


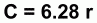
This equation should look familiar.
In fact, it's just the formula for the circumference of a circle.

The value of  pi is approximately  3.14, so the number  6.28
must represent  two times pi:


And there is the result ... the equation of the line found by graphing the radius and circumference for various circles gives a linear function, which is the formula for circumference using  r.


What we've just done is relate what you know about lines from your study of coordinate geometry to the circle circumference formula. There are all sorts of connections between ideas in math, just like this one.


Resources


Content, HTML, graphics & design by Bill Willis 2023