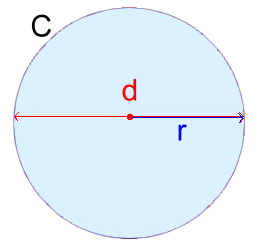
 
The circumference of a circle C is the distance all the way around the outside.In order to calculate that distance, we'll need to know the circle's radius r, or the circle's diameter d. The diameter is twice as long as the radius: d = 2·r We'll also need to use π. You can learn more about π here. Because the value of π appears whenever you divide the circumference of a circle by its diameter, we can write this fact using symbols: π = C/d Rearranging this we get C = π·d (We use a dot for a 'times' sign in formulas, rather than an 'x', to avoid confusion). This is a formula we can use to calculate the circumference of a circle. Let's try an example.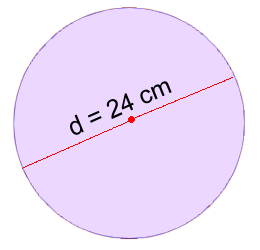 
Example 1:C = π·d C = π x 24 Use the π button on your calculator C ≈ 75.4 cm approximate because we had to round it. π is an Irrational number. Example 2: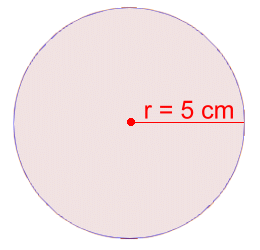 
Here we're given the radius. We could just double this to get the diameter, or we could use a different formula:Because d = 2·r, the formula C = π·d becomes C = π(2·r) or C = 2·π·r C = 2·π·r C = 2·π(5) C ≈ 31.4 cm
You can also use these formulas to find d or r, if you know the circumference.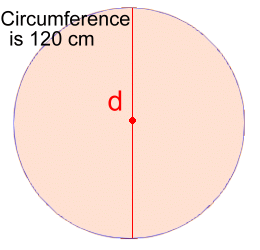 
Example 3:The circumference is 120 cm. Find the diameter. C = π·d 120 = π·d 120 ÷ π = d 38.2 cm ≈ d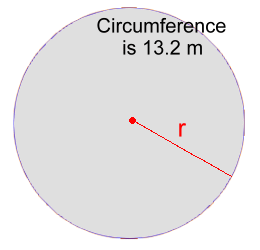 
Example 4:The circumference is 13.2 m. Find the radius. C = 2·π·r 13.2 = 2·π·r 13.2 ÷ 2 ÷ π = r 2.1 m ≈ r There are all sorts of problems you can solve using these formulas: Example 5: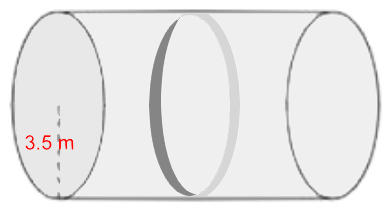 
A cylindrical industrial tank with radius 3.5 m needs a strengthening band attached around the middle. How long is the band?Its length is the circumference of the cylinder. C = 2·π·r C = 2·π(3.5) C ≈ 22.0 m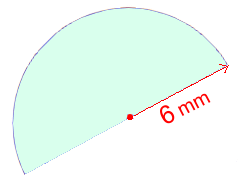 
Example 6:A semicircular piece of metallic jewellery will have a gold wire attached all the way around. How long must the wire be? There are several distances we must calculate: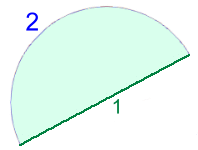 
Distance 1 is just twice the radius. This is 12 mm. Distance 2 is half the circumference of the circle: C÷2 = 2·π·r ÷ 2 = 2·π(6) ÷ 2 ≈ 18.8 mm So the total distance around is 12 + 18.8 ≈ 30.8 mm |