Page Two How to Recognize Congruent Triangles If you are given information about corresponding sides and angles that are equal in two triangles, there is a minimum amount of information in a certain pattern that must be true, in order to conclude that the triangles really are identical. Here's the first example: 1. SAS 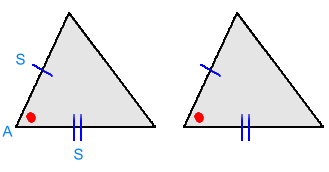Notice the pattern of the information we are given: In order: equal sides - equal angles - equal sides SIDE - ANGLE - SIDE   This is the SAS shortcut. When presented with this information, you can conclude that the triangles are congruent, and that all the other sides and angles are equal too! 2. AAS 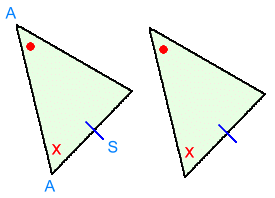Notice the pattern of the information we are given: In order: equal angles - equal angles - equal sides ANGLE - ANGLE - SIDE   This is the AAS shortcut. When presented with this information, you can conclude that the triangles are congruent, and that all the other sides and angles are equal too! 3. ASA 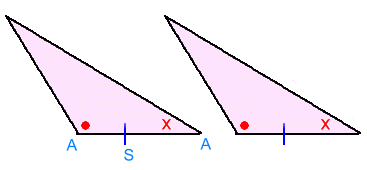Notice the pattern of the information we are given: In order: equal angles - equal sides - equal angles ANGLE - SIDE - ANGLE   This is the ASA shortcut. When presented with this information, you can conclude that the triangles are congruent, and that all the other sides and angles are equal too! 4. SSS 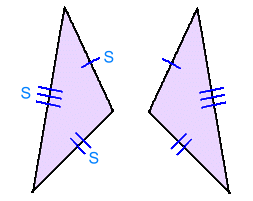Notice the pattern of the information we are given: In order: equal sides - equal sides - equal sides SIDE - SIDE - SIDE   This is the SSS shortcut. When presented with this information, you can conclude that the triangles are congruent, and that all the other sides and angles are equal too! 5. HS 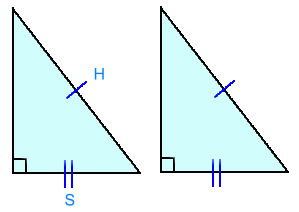Notice the pattern of the information we are given: In right triangles: equal hypotenuses - equal sides HYPOTENUSE - SIDE   This is the HS shortcut. When presented with this information, you can conclude that the triangles are congruent, and that all the other sides and angles are equal too! ----------------------------------------------------------------------------------- Before we look at some problems involving congruent triangles, here are two non-shortcuts to watch out for: 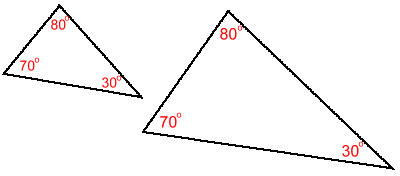1. AAA does not prove triangles congruent Here are two triangles that are obviously not congruent; being different sizes (having different corresponding side lengths), they aren't identical. Two triangles with all the corresponding angles equal are NOT necessarily congruent. 2. ASS does not prove triangles congruent We won't bother with a diagram. This one is easy to remember. Now let's look at some congruent triangle problems >>> Page One | Page Two | Page Three Resources Content, HTML, graphics & design by Bill Willis 2024