 
Finding a Missing Angle Example 3: Find angle θ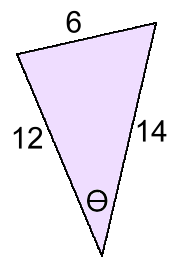 
cosθ = a2 + b2 - x22 a·b X is the side opposite θ cosθ = 122 + 142 - 62 2 12·14 cosθ = 0.9048 θ = 25° rounded to nearest whole degree Sometimes the missing angle will be obtuse. This adds an extra step. Example 4: Find angle θ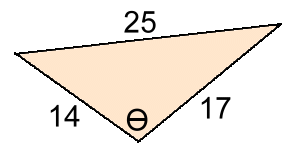 
cosθ = a2 + b2 - x22 a·b X is the side opposite θ cosθ = 142 + 172 - 252 2 14·17 Here's where this one is different. cosθ is negative. cosθ = = - 0.2941 This means θ must be larger than 90°. Because the total of the three angles in a triangle must be 180°, the missing angle θ can only be in the second quadrant. Find the reference angle θr first: θr = cos-1 (0.2941) = 73° rounded to nearest whole degree θ = 180 - 73 = 107° The cosine law, as well as the sine law, can also be used on right triangles. However, it's quicker and easier to use regular trig functions for those, saving the sin and cos laws for non-90° triangles. |