Penguins hang out together by the tens of thousands. When a biologist wants to count all the penguins on a beach, he has a big problem. Not only are there a whole lot of penguins ... but they're constantly leaving and arriving by the hundreds every minute. This makes the job of counting them next to impossible.

Unless you use a camera, and a little statistics!

First the biologist takes an arial photograph of all the penguins on the beach.
It might look something like this:

Here's a real photo:


With a magnifying glass and some patience, you might count them. But this is only a few hundred penguins; a photograph of all the penguins on a beach could contain many thousands of them! Too many to count!!

We're going to work with a diagram instead:


What the biologist does first is divide the photograph up into small, equally sized segments using a ruler and a pen. In our photo of the 'penguins', we've done that. There are 66 segments.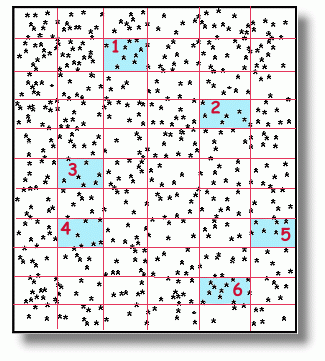

Now here's the interesting part. What happens next is that some segments are randomly picked to count. We decided to pick six segments, and chose them at random. In actual practice, a random choice could be made by closing your eyes and dropping a small pebble onto the photograph. A better way is to assign each of the 66 segments a number, and have a random number picked on a computer or a calculator. (A Ti84 will do this!) Here are my six selections, numbered one to six:

Now count the penguins in each segment. If a penguin is on a line, count it as half a peguin.
SEGMENT NO. OF PENGUINS
1 9.5
2 6.5
3 6.5
4 6
5 6
6 11

The next step is to average these values. Add the six numbers, and divide by six.
This gives us an average of 7.6 penguins per segment.

If you go back and look at our 'photograph' with the lines drawn on it, you'll discover there were 66 segments. If each one has, on average, 7.6 penguins in it, then the total number of penguins in the photograph should be

66 X 7.6 = 501.6
or about 502 penguins!

This procedure can be used to count any large number of things where you can see them all in a photograph.

Remember, this method is only statistical, so it only gives an approximate answer. But the more 'sample' segments you use, the more accurate it gets!

How close did we come to the right answer? Well, we'll let you go back to the original picture and count the penguins yourself!

Main Page