 
The problem we are presented with is to find out how much water is flowing through a culvert in a given amount of time. The answer should be an amount in cubic metres per second, which could then be converted to other units as desired. We are able to make some simple measurements at the culvert: - distance to the surface of water, from the top of culvert - radius of the culvert - length of the culvert - width of the water surface in the culvert In addition, we can fairly easily work out the rate of flow, in metres per second. With all of this data, we'll show you how to make an estimate of the volume of water flowing through the culvert in cubic metres per second. 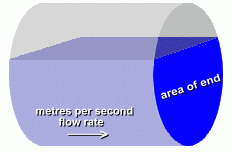 There is a standard formula for calculating the rate of quantity flow for a stream, pipe, or culvert: Quantity (m3/s) = water velocity (m/s) x cross-sectional area of water (m2) We'll need to know how fast the water is moving, and the cross-sectional area of water in the culvert. (For simplicity, it will be assumed a perfect cylinder) Velocity of the Water: We don't have a device for measuring this, but it is fairly easy to calculate. We'll drop something in the water at one end of the culvert, and time how long it takes to reach the other end. Kenneth is going to help us with these measurements.    The length of the culvert is 20 metres. The object dropped into the water took about 100 seconds to travel this distance. This makes the velocity of the water approximately 20 m in 100s, or 0.2 m/s Area of the Water in the Culvert  At the beginning, we said we'd make an estimate of the amount of water flowing through the culvert. Unfortunately, the exact formula for the cross-sectional area of water in a hemispherical pipe is quite complicated ... far too difficult to try to explain or use here. In addition, its use requires angle measurements which would be difficult to obtain in a culvert full of water.So instead we'll make an approximation of this area, the area shown in the diagram in blue, at the right, which represents the area of the water in the pipe for a culvert more than half full. This calculation is shown below.  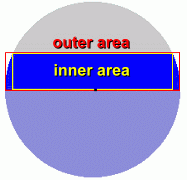 The difficulty lies in calculating the area of the light blue segment, which has curved ends. The formula for this area is too complicated to make use of here. Instead, we'll find the area of the outer and inner rectangles surrounding this segment, and average the two. The answer will be quite close to the actual area of the segment. Let's do the calculations with variables first, to obtain a formula. Then we'll use the actual measurements from the water in the culvert to calculate its area.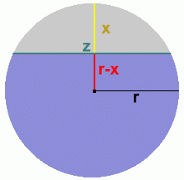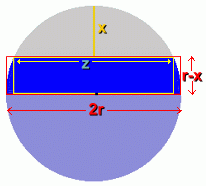  
r is the radius of the cylinderx is the distance from the top of the culvert, down to the surface of the water. r-x is the difference between the radius and the number above (or the water's height above the cylinder's centre) z is the width of the surface of the water in the culvert. The dimensions of both the outer and inner rectangles are shown at the right. We want to average them. 
At the right is the calculation showing the total cross-sectional area of the water in the culvert, including both the half-circle below, and the approximation for the area above centre. The half-circle below centre has the area formula A = (pi · r2)/2 Both the outer and inner rectangles have the area formula A = L x W We are adding these two areas, and dividing by two to average them. In the last step, we factored out the (r-x) to make the final formula a little simpler to work with. Now let's use it with the actual culvert measurements ...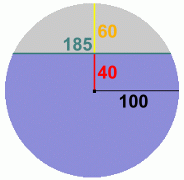  
At the left are the measurements we made of the actual culvert, in centimetres.At the right is the formula with the actual values filled in; this gives us the total cross-sectional area of the water in the culvert. Although this value is an approximation, it is certainly close enough for our purposes. Area of water in pipe = 2.34 m2 Now let's go back to the formula for calculating the rate of quantity flow for a pipe: Quantity (m3/s) = water velocity (m/s) x cross-sectional water area (m2) Q = V · A = 0.2 m/s x 2.34 m2 = 0.47 m3/s or about half a cubic metre, per second. 0.5 m3 per second corresponds to 30 m3 per minute, or 1800 m3 per hour. This is equivalent to about 63,500 cubic feet per hour, or about 1,060 cubic feet per minute, or approximately 6600 gallons per minute. Here are some conversion factors you might find useful:
|