Volume of a Cylinder 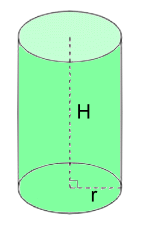V = area of base x height V = (πr2) x H Volume = π·r2·H Example 1: Find the volume 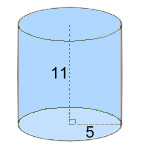V = π·r2·H V = π·52·11 V = 863.9 cm3   rounded to 1 d.p. Example 2: The volume is 890 cm3. Find the height 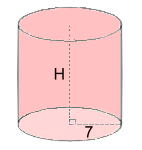V = π·r2·H 890 = π·72·H 890 = 153.94·H 5.8 = H   rounded to 1 d.p. Example 3: The volume is 1800 cm3. Find the radius 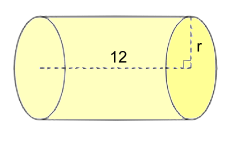V = π·r2·H 1800 = π·r2·12 1800 = (37.70)r2           1800/37.70 = r2           48.65 = r2 ... now do a square root:           7.0 = r   rounded to 1 d.p. Surface Area of a Cylinder 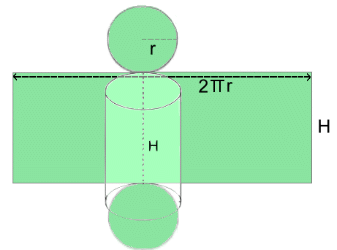The surface area formula has three parts: TOP: circle area π·r2 BOTTOM: circle area π·r2 CENTRE WRAP-AROUND SECTION:    This is a rectangle:    - Its length is the distance around, which is      the circumference of a circle: 2·π·r    - Its width is H   So its area is 2·π·r·H   Surface Area = 2·πr2 + 2·π·r·H Example 4: Find the surface area SA = 2·πr2 + 2·π·r·H SA = 2·π·52 + 2·π·5·11 SA = 502.7 cm2   rounded to 1 d.p. Example 5: The surface area is 1000 mm2. Find the height 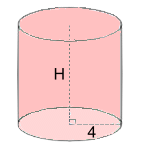SA = 2·πr2 + 2·π·r·H 1000 = 2·π42 + 2·π·4·H 1000 = 100.53 + 25.13·H 899.47 = 25.13·H 35.8 mm = H Example 6: 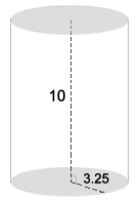What are the area and dimensions of the label    on a Campbell's soup soup can? This is the wrap-around portion of the formula:    SA = 2·πr2 + 2·π·r·H    SA = 2·π·r·H    SA = 2·π·(3.25)·10    SA = 204.2 cm2 The dimensions are its width and length: Width = height = 10 cm Length = 2·πr = 2·π(3.25) = 20.4 cm Resources Content, artwork, HTML & design by Bill Willis 2024