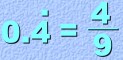Decimals .........

Changing Repeating Decimals to Fractions
When the Entire Decimal Repeats
When changing a terminating decimal to a fraction, the bottom of the fraction was a '1' and some zeros.

For example: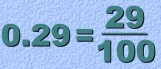

But, when the decimal is a repeater, the bottom will be nines!
There is one 'nine' for every repeating digit.

Here's an example: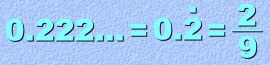

Notice that only a single '2' repeats. So the fraction is a '2' over a single '9'.

Here are two more examples:

Here just a single '7' repeats.
So the fraction is a '7' over just one '9'.

In this example, only '4' repeats.
The fraction is '4' over a single '9'.

If more than one digit repeats, then the fraction will be over more than one '9'.

For example:

In this case, the digits '17' repeat over and over. So the fraction is '17' over two nines.

Here are two more like that. Notice again that these are over two nines because two digits repeat: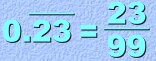

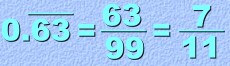And once again, if the fraction you get can be reduced, you must reduce it.

Here's a final example with three repeating digits. So of course the fraction will be over three nines: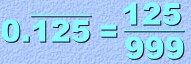

Here is the rule, summarized one more time:

'If the entire decimal number repeats, the corresponding fraction
is that number over the same number of nines.'

Decimals & Fractions Menu