|
Ordinary decimals are the ones you are already familiar with. Ordinary decimals are more commonly called terminating decimals, because they end. For example, 0.25 is a terminating decimal The decimal 0.725 is terminating decimal, because that's all there is. Every terminating decimal can be turned into a fraction. The decimal 0.4333... isn't 'terminating'. The '3' at the end repeats over and over, forever. This kind of decimal is called a repeating decimal. Repeating decimals can be turned into fractions too. More about that later. This page will review how to change a terminating decimal into a fraction. (You should know how to do this already. But the new methods we'll be showing you later are similar, so the review will be useful). Changing a Terminating Decimal to a Fraction: This method is very simple: The decimal number becomes the top of the fraction, and the bottom is 10, 100, 1000, ... a '1' with the same number of zeros as the number of decimal places in the original decimal. For example: 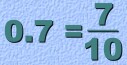 One decimal place ... one zero. So 0.7 becomes 7 over 10. Here's another one. Notice that the fraction you get must always be reduced: 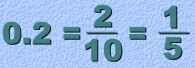 If there are two decimal places, then the fraction will be over 100: 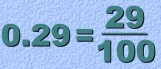 And three decimal places means the fraction will be over 1000: 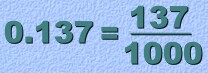
That's it! Here's the rule again, just to make sure you've got it: "For a terminating decimal number, the fraction is made from the number part on top, and a power of 10 on the bottom ... one zero for every decimal place." |