|
When Only Part of the Decimal Repeats Here is an example of a repeating decimal where only part of the decimal repeats: There is one digit that repeats, and two digits that don't. Here's one more example: There are two digits that repeat, and there is one digit that doesn't. Now let's look at how to change these partially repeating decimals into fractions. The method requires the repeating decimal be in the form with the dot over or bar over the repeating digit(s). Here's another partially repeating decimal:  Notice that it contains one repeating digit (2), and two non-repeating digits (34). Here's how to make the fraction, using the decimal with the dot over the repeating part:
This gives a final answer of 308 over 900, which can be reduced: 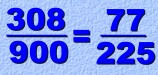 Let's look at another one.  In this example, there are two repeating digits, and one non-repeating digit.
Here's another one:  Notice that it contains one repeating digit, and two non-repeating digits.
Here's a final example, just to make sure you've got it.  This one contains two repeating digits, and two non-repeating digits.
Now look at this additional example; see if you can identify the steps that were carried out.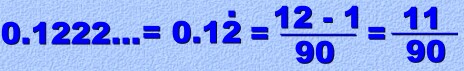 
|
Incidentally, you can always check your calculation by dividing your final fraction on a calculator...