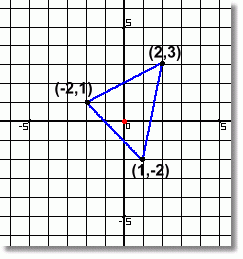
 Here is a triangle drawn on a set of axes. The corners are labelled, and the centre of dilatation will be the origin, which is (0,0).
Once again, we'll show a dilatation that is an enlargement of factor 2.
Just as before, we will need to draw lines from the centre of dilatation, through each of the corners of the figure. Then we will need to identify new points that are twice as far from the centre.
(You can also shrink a figure just as easily. In that case, if the factor were 1/2, you would find points that were only half as far from the centre. We're leaving those for you to try on your own!)
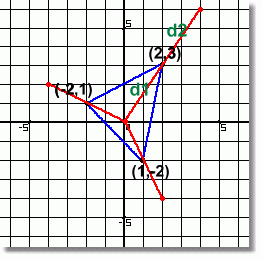
Here is the diagram with the lines drawn through the three corners of the triangle. We've put red dots at the locations that are twice as far from the centre. As an example, look at the top right point of the triangle. The new image point is twice as far away.
Distance d2 is the same as distance d1.
Now let's draw the triangle and check that it is correct...
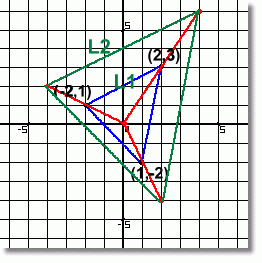 Here is the image, shown in green. It seems to have the same shape and orientation as the original figure. We can check that it really has been enlarged by a factor of 2 by measuring the corresponding sides, which should now be twice as long. Shown here as an example, side L2 is twice as long as side L1.
This worked exactly the same as the one we did on page 1. But there's a difference. When you are doing a dilatation on a set of x-y axes with the point (0,0) as the centre of dilatation, there is a great shortcut you can use. It will be obvious when we identify the image points below.
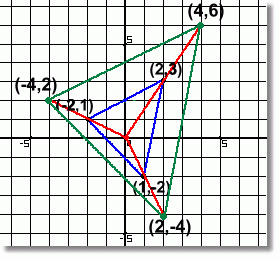
Look closely at the original points, and what they became when we did an enlargement of factor 2 from the point (0,0).
(2,3) ···> (4,6)
(-2,1) ···> (-4,2)
(1,-2) ···> (2,-4)
Do you see what happened?
Enlarging the figure by a factor of 2 caused all the point coordinates to double!
This always happens when the centre of dilatation is the origin (0,0).
For example, the point (5,11), if we were doing a dilatation of factor 4, would become (20,44)
You can find the image points for any dilatation without drawing and measuring!
One more example: the image of (12,15) for factor 1/3 would be the point (4,5).
This only works if the centre is (0,0).
|
