 Part 2: Fractions With Different Denominators (part 2) The fractions are made from pieces that are NOT the same size, and both have to be changed. Example 3: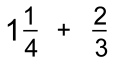 
Not only are the denominators different, but you can't make them the same by changing just one.Let's make the first fraction improper first: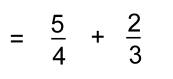 
In order to combine pieces, you'll have to use what you learnedabout equivalent fractions. We can change both to equivalent fractions of twelfths. Here are the pictures: 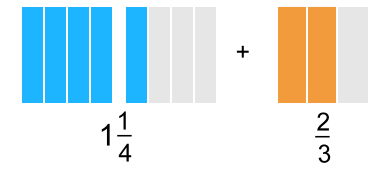 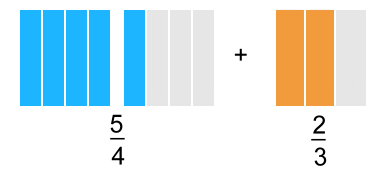 We need a common denominator for 4 and 3. The smallest one is 12. Multiply the first fraction by 3 and the second by 4: 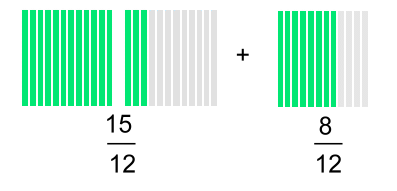 Now we can add all the 'twelfths' pieces: 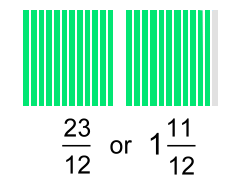 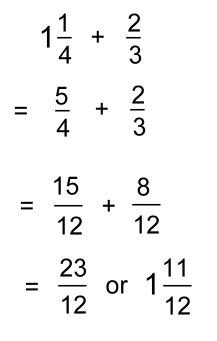 In words: "One and one quarter plus two thirds is the same as five quarters plus two thirds which get changed to fifteen twelfths plus eight twelfths resulting in twenty three twelfths or one and eleven twelfths". Example 4: Let's do the last example without pictures! 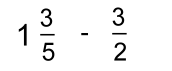 First we'll change 1 3/5 to 8/5: 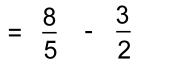 We need a common denominator for 5 and 2 The smallest one is 10. Multiply the top and bottom of each fraction by a number that will make an equivalent fraction over 10. The first fraction will be multiplied by 2; the second by 5: 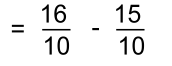 Once they're both 'tenths', they can be subtracted: 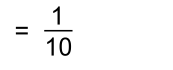 |