 Limit notation is a mathematical notation used to describe the behaviour of a function as the input approaches a certain value. It can be used to describe the behaviour of the graph of a function as it approaches a certain point, such as a maximum or minimum. Here we'll review the limit rules that you've learned, with some examples. The methods shown here will be shortcuts, rather than the formal evaluations. Finding the exact value of a limit: In the simplest case, you can just substitute the limiting value into the expression and work it out: 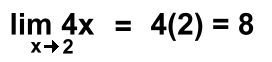 In words: "As x approaches 2, the value of the expression 4x approaches 8" Here's the general rule: 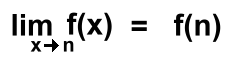
An alternate way to exaluate these might be to extract the constant: "As x approaches 2, the value of the expression 4x is four times the value of the expression x" 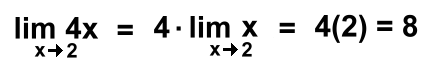 Here's the general rule: 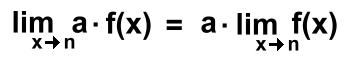
Indeterminate Limits: Sometimes when you evaluate a limit, you can't get an answer. Here we're filling in 2: 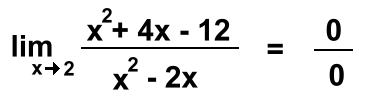 0/0 has no answer. We'll need a different strategy when this happens. Start by factoring the top and bottom: 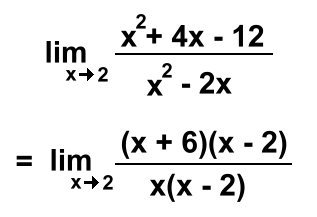
Simplify: 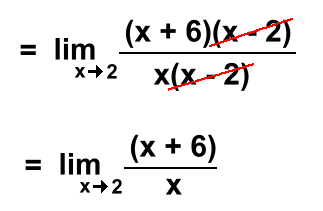
Now you can evaluate it by filling in the 2: 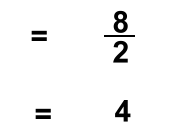
Let's move on to limits where the limiting value is infinity; visit page two ... |