Distance From a Point to a Line ....................................

Method 1: Find the Equations of Both Lines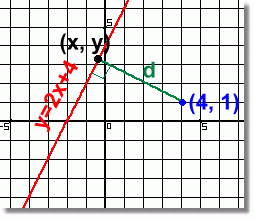

Using this method, we'll first find the equation of the line represented by distance d.

Then we'll find the intersection of that line with the line y=2x+4, which will give us point (x, y).

Finally we'll use the distance formula to find the required distance d between (x, y) and (4, 1).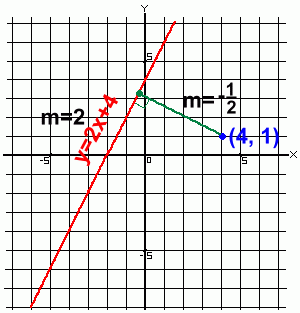

Step 1:
Find the equation of the line represented by distance d

The slope of y=2x+4 is 2, so the slope of the line representing distance d must be -1/2, since it's perpendicular.

The line representing distance d has slope -1/2 and passes through the point (4, 1).
We can find its equation using the point-slope formula for the equation of a line:

y - y₁ = m(x - x₁)
y - 1 = (-1/2)(x - 4)
y - 1 = -1/2x + 2
y = -1/2x + 3

Step 2: Find the intersection point of the two lines.

y = -1/2x + 3
y = 2x + 4

Solve by comparison:

-1/2x + 3 = 2x + 4
-x + 6 = 4x + 8
-5x = 2
x = -0.4

y = 2(-0.4) + 4
y = 3.2

The point (x, y) where the lines
intersect is (-0.4, 3.2)

Step 3: Find the length of the line representing distance d

Find the distance between (-0.4, 3.2) and (4, 1):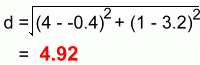

Method 1 gives an answer of 4.92 for the distance from point (4, 1) to the line y=2x+4

BACK