 Method 3: Find the Area of a Triangle Using Coordinates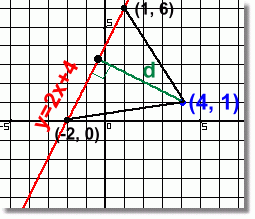 
Using this method, we'll first find two points on the line y=2x+4 that form a triangle with point (4, 1), where distance d is an interior height of the triangle. We'll then use a formula to find the area of the triangle using the three points. Finally, we'll work out the base length and use the area to solve backwards for the height d.
[There are some problems with this method. The selection of points 'by inspection' shown below won't always work so nicely. And the area formula used is not in high school math] Step 1: Find two points on the line. By inspection, we chose x values of -2 and 1 as likely values to make the required triangle. Substituting each into the line equation gives points (-2, 0) and (1, 6). We now have the coordinates of the three corners of the triangle: (-2, 0), (1, 6) and (4, 1) Step 2: Find the area of the triangle. This formula is one which you probably haven't seen before. Given the three coordinates of a triangle (x1, y1), (x2, y2), (x3, y3) the area is given by A = | (1/2)(x1y2 + x2y3 + x3y1 - x2y1 - x3y2 - x1y3) | Using this formula with the points we have: (x1, y1), (x2, y2), (x3, y3) (-2, 0), (1, 6), (4, 1) A = | (1/2)(x1y2 + x2y3 + x3y1 - x2y1 - x3y2 - x1y3) | A = | (1/2)(-2x6 + 1x1 + 4x0 - 1x0 - 4x6 - -2x1) | A = | (1/2)(-33) | A = | - 16.5 | A = 16.5 Step 3: Find the base of the triangle. This is the distance between points (-2, 0) and (1, 6)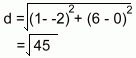 
Step 4: Find the height of the triangle. We now know the area and base of the triangle. We can solve for the height d 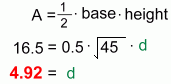 Method 3 gives an answer of 4.92 for the distance from point (4, 1) to the line y=2x+4 |