 Method 4: Find the Area of a Triangle Using Heron's Formula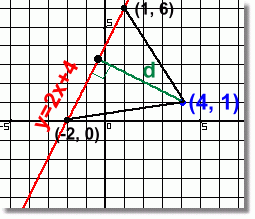 
In this method, we will again find two points on the line that form a triangle, where d is the height. We'll find the area of the triangle a different way, and then solve for the height. [There are some problems with this method. The selection of points 'by inspection' shown below won't always work so nicely. And the area formula used is again not in high school math] Step 1: Find two points on the line. By inspection, we chose x values of -2 and 1 as likely values to make the required triangle. Substituting each into the line equation gives points (-2, 0) and (1, 6). We now have the coordinates of the three corners of the triangle: (-2, 0), (1, 6) and (4, 1)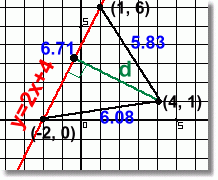 
Step 2: Find the length of each side.Using the distance formula (we won't show the work this time) on each pair of points, the three sides of the triangle have lengths as shown on the diagram. Step 3: Find the area of the triangle. Heron's formula for the area of a triangle is: 
where a, b, c are sides of the triangle,and  Using a = 6.71, b = 5.83, and c = 6.08 for the sides, calculating s yields s = 9.31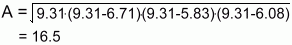 
Step 4: Find the height of the triangle. We now know the area (16.5) and base (6.71) of the triangle. We can solve for the height d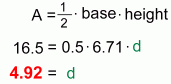 
Method 4 gives an answer of 4.92 for the distance from point (4, 1) to the line y=2x+4 |