 Mildred was telling me about really big numbers she'd learned about from her teacher. "A googloplex is gigantic" she told me. "It's so big that you can't even write it out!" "There are lots of big numbers", I told her, "Some even bigger than googolplexes!" I asked her if she knew about exponents. She did, although she hadn't covered that in school yet. "Exponents can lead to some pretty big numbers fairly quickly", I told her. "Here's an example: 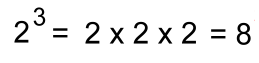 "In this power of two, the exponent '3' raised on the right tells you how many 'twos' get multiplied together". "With an exponent of just 10, we're already at over 1000: 210 = 1024 "Similarly, powers of ten can get very large too. The Earth, for example, has a mass of 6 octillion grams, or 6 x 1024 grams". Mildred jumped in: "A googol is 10100. A whole bunch larger! And a googolplex is 10googol, or 1010100. It's huuuuge!!" I told her she could find out more about googols and googolplexes here. I kept going. "To get such big numbers, we need larger and larger exponents. With tetration, that isn't the case!" "Tetration?? I've never heard of it!" Mildred stated. I responded: "Here's a simple example of tetration: "Notice that the 'exponent' is on the left!" "This number raised on the left tells you how many times 2 is repeated as an exponent". 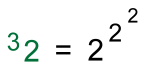 2 is called the base. 3 is called the height of the tetration. 32 is read as the third tetration of 2 "These are always evaluated from the top down": 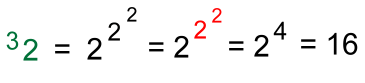
"Here's another example, with the height again 3": 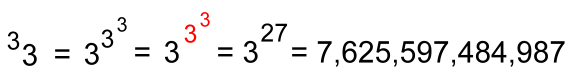
"As you can see, these can get very large results with just small bases". "Here's another one with height 3": 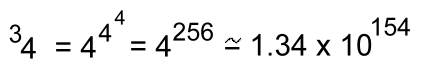 "With the base just 4, a tetration with height 3 gives a result that is incredibly large, far bigger than a googol or anything meaningful that we can describe". "If we move up to base 10, with height 3": 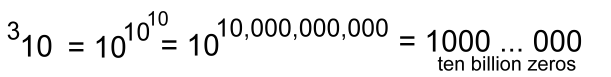 "... another unimaginably large number ... bigger than the total number of atoms in the known universe!" "Compare this to the ordinary power with base 10": 103 = 1000 Mildred said: "Let's try one with height 4, and base 2": 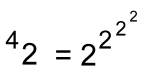 Working from the top down: 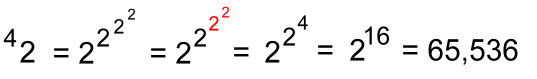
"Notice how much larger tetration is compared to exponents" I said: Exponents: 24 = 16 Tetration: 42 = 65,536 "Let's try another one, still with height 4, but with base 3": 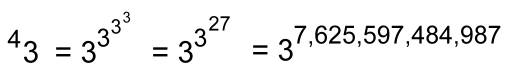
"We can't work this one out because the result is so large that our calculator can't do it!" Mildred was impressed by that. "Let's move up a level, back to base 2, but height 5" I suggested: 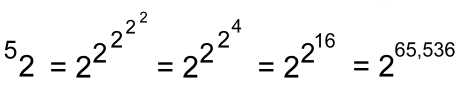 "The result, rounded and using scientific notation, is 2 x 10 19,728, once again a number that is so big it defies meaningful description". Mildred didn't know about scientific notation, so I explained it to her. You can learn about it here. I told Mildred: "Let's stop here. This can be continued to get larger and larger numbers, but we've already encountered numbers that have no meaning in the real world. You can see now why tetrations are not discussed in high school or even university math, as they quickly lead to values that are too big to be useful for anything real, even in the realm of astronomy". |