 The midpoint of a line is the point M (x, y) that is half way between the two endpoints of the line. We'll show you how to find the midpoint, and to solve problems where you know the midpoint and one endpoint and are asked to find the other.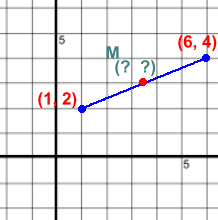 
We'll start with a line in the first quadrant where all the values are positive.The two endpoints (1, 2) and (6, 4) are shown. We estimated the position of M and labelled it. The midpoint is the point M (xm, ym) where xm and ym are the averages of the x and y endpoints. By 'average' we refer to the mean. For example, the mean of 6 and 10 is (6+10)/2, which is 8. You can review the concept of 'mean' here. The midpoint is a point M (xm, ym) where xm is the mean of the x values of the endpoints, and ym is the mean of the y values of the endpoints. Since there are two endpoints, the mean is what you get when you add two numbers and divide by 2. Here's the midpoint definition as a formula: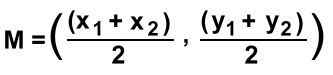 
where:x1 and x2 are the x values of the two endpoints y1 and y2 are the y values of the two endpoints Let's go back to our opening example. The endpoints were (1, 2) and (6, 4) We get the midpoint by averaging the x's and y's: 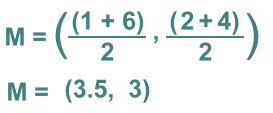 Let's try another one.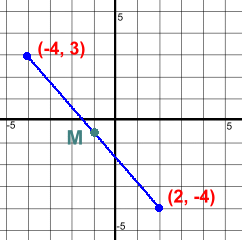 
The endpoints are (-4, 3) and (2, -4)We estimated the midpoint position. The midpoint calculation: 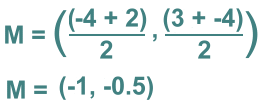 The reason for estimating the position of M first is so we can check our answer; if we'd made a mistake the answer would likely be way off. Let's do one more without a graph: Find the midpoint of the line joining (-5, -2) and (1, 4). Solution: M = [(-5 + 1) , (-2 + 4)] 2 2 M = [-2, 1] where we used square brackets for clarity. If you use a calculator to work out each part, you'll need the brackets, like this: (-5 + 1) and (-2 + 4) 2 2 Now let's try some problems where you have to find an endpoint ... |