 Here is an assortment of problems from Math 8, Math 10 and Math 30, where multiple concepts are a part of each problem, or used in the solution. Clearly, algebra plays a large part in solving most problems, but sometimes the solutions can be a little unusual when you are dealing with, for example, trigonometry and logarithms in the same problem! Problem 1: Math 8 [geometry + algebra] 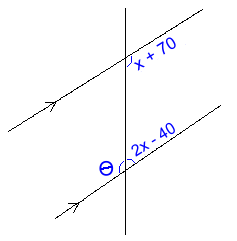
Find θ Solution: The two angles on the right of the transversal are supplementary: 2x - 40 + x + 70 = 180° 3x + 30 = 180 3x = 150 x = 50 This makes angle 2x - 40 equal to 2(50) - 40 = 60° The supplementary angle θ = 120° Problem 2: Math 10 [measurement formulas + algebra] 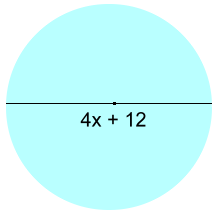
Find the area of the circle Solution: Area = πr2 The radius is 2x + 6 A = π(2x + 6)2 A = π(4x2 + 24x + 36) Problem 3: Math 30 [logarithms + trigonometry] Solve for θ if 0 < θ < π/2: 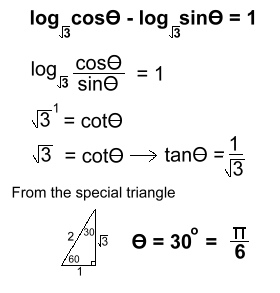
Problem 4: Math 30 [factoring + trigonometric identities] Simplify: sin4θ - cos4θ (sinθ - cosθ) = (sin2θ + cos2θ)(sin2θ - cos2θ) (sinθ - cosθ) = 1·(sin2θ - cos2θ) (sinθ - cosθ) = (sinθ + cosθ)(sinθ - cosθ) (sinθ - cosθ) = sinθ + cosθ Problem 5: Math 30 [algebra + quadratic equations + logarithms] Solve: 2log2x - log2(x + 3) = 2 log2x2 - log2(x + 3) = 2 log2 x2 = 2 (x + 3) 22 = x2 (x + 3) 4 = x2 (x + 3) 4x + 12 = x2 x2 - 4x - 12 = 0 (x - 6)(x + 2) = 0 x = 6 or x = -2 x = -2 gives a log of a negative, so the only answer is x = 6 |