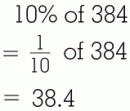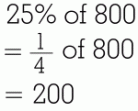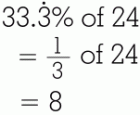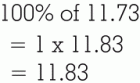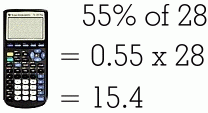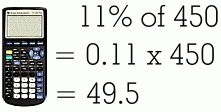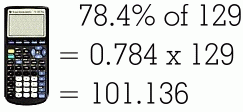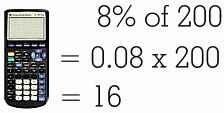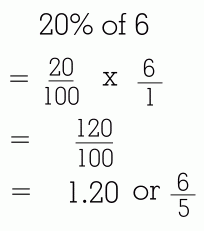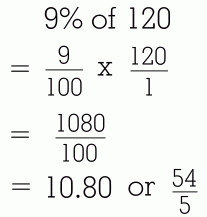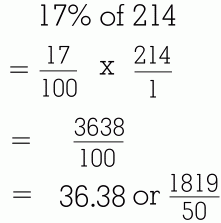This page will show you three ways to do this problem. In order to understand what we'll show you, you need to understand what percents mean, and how to convert them to decimals or fractions. You also need to be able to reduce fractions. You also need to understand that when you find a percent of something, the answer has the same units as the number you are finding the percent of. For example: Now let's look at the three methods for finding a percent of a number: Method 1: The Quick and Easy Way: 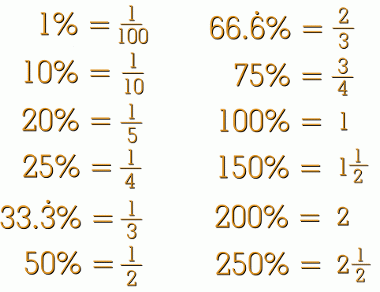
The easiest way to find a percent of a number is to know the fractional equivalent for some common percents. At the right are some of these often-used percents and the fractional value for each. You'll need to memorize these. Method 1 involves using the fraction instead of the percent. For example, if you were asked: you would instead ask yourself: This makes it easy to get the answer 18. The advantage of this method is that it is fast ... faster even than using a calculator. This will be a big advantage in later Math courses where you won't have a lot of extra time to do basic calculations. Here are some more examples:
One drawback of this quick method is that you will need to memorize some conversions. But your teacher will expect you to know them anyway, so that's nothing to worry about. The other drawback is that the quick method won't work for percents for which you don't know the fraction, or for which the fraction isn't a simple one. It also won't work if the calculation is too difficult to do in your head. But watch out for special cases where you can reverse the quetion. For example, you probably can't do 80% of 50 in your head. But the answer will be the same if you reverse it: try 50% of 80. It's obviously 40. Watch out for questions where this trick will work! However, if you were asked to find 29% of 123.9, the quick method isn't very useful. You're unlikely to be able to do twenty-nine hundredths of 123.9 mentally. For problems like this, which are the kind you're most likely to encounter in real life, we need a new method. Method 2: Using Decimals and a Calculator: 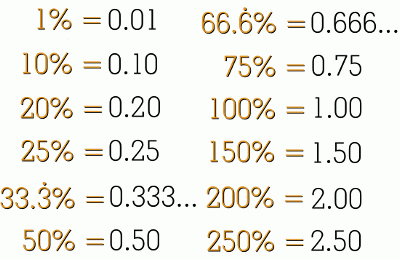
This method requires that you either know the decimal value for the percent, or can find it. Fortunately it is very easy to change a percent to a decimal. Since a percent is really just a fraction over one hundred, you will really be dividing by 100, which means you just need to move the decimal point two places to the left. In order to do a question like this: you must convert 28% to 0.28 by moving the decimal back two places. Then you use a calculator, remembering that 'of' means that you multiply: Here are some more examples. Remember that you can always use the calculator on your phone!
This method isn't quite as fast as the previous one. It's big advantage is that is will work for every question you encounter. You just need to be able to convert the percent to a decimal so you can enter it on your calculator. Method 3: Using Fraction Operations:
This method takes longer, and requires more effort. You may still require a calculator to do the multiplication. However, this is a valuable method to learn, because it is something you will find useful in later High School courses. Here are a few more examples of Method 3. Follow each step carefully and make sure you understand what we did.
|