|
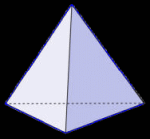
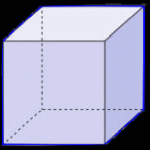
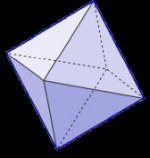
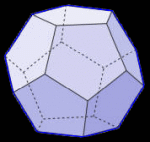
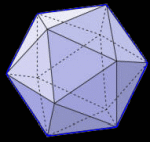
A polyhedron is a 3-dimensional closed figure made from flat sides, or 'faces'. There are an infinite number of them. A barn, for example, has many flat surfaces or faces; it's a polyhedron. So it a textbook. A prism. The diamond in a ring. All these figures are made from flat 'faces'. But on each one of the objects mentioned above, some of the faces are different sizes. Some are different shapes. Is there a polyhedron with all the faces the same? You're probably already familiar with flat 2D shapes called polygons where all the sides are the same. They're called regular. A square is a regular quadrilateral. An equilateral triangle has three identical sides. A regular hexagon looks like the cell in a bee hive. Three dimensional shapes made from flat faces can be regular too. For example, a box of tissues is a 6-faced prism called a hexahedron. If all the faces were identical, they would all be squares, and that regular hexahedron would be called a cube.  The actual name is based on the number of faces; it's a regular hexahedron' Are there any other regular polyhedra? Yes there are. But, including the cube, there are only five of them! If the sides are squares, you can make a hexahedron (cube). If you use equilateral triangles instead, you can make three other 'regular' polyhedra ... the tetrahedron (4 equal faces), the octahedron (8 equal faces), and the icosahedron (20 equal faces). There is also a polyhedron made from regular pentagons. It has 12 faces, all regular pentagons, and it's called a regular dodecahedron. 
These are the only regular polyhedra that exist! No other 3-dimensional object with flat surfaces can exist and be made from surfaces that are all the same. Here are the five regular polyhedra with a description of each.
|