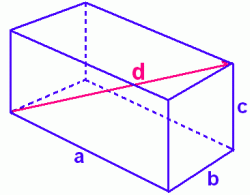
  The Pythagorean Theorem, which allows you to find the hypotenuse of a right triangle, can also be used in three dimensions to find the diagonal length of a rectangular prism. This is the distance d from one corner of the box to the furthest opposite corner, as shown in the diagram at the right. 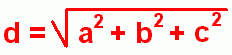 But a much more interesting and useful application of the Pythagorean Theorem in three dimensions is to find the distance between any two points in 'space' (as opposed to points on a flat surface). You may not be familiar with graphs of points in three dimensions; it's a topic usually reserved for advanced math in the final year of high school (in Alberta, Math 31). But it's easy to understand. Let's look at a three-dimensional graph ... 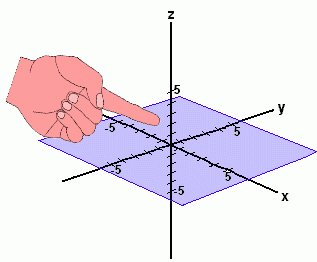 In the picture on the right, the light blue region represents the familiar x-y axes on which you would graph a two-dimensional relation, such as a line or parabola. All such graphs are flat; they lie in a single plane, or flat surface, which is two-dimensional. In the picture on the right, the light blue region represents the familiar x-y axes on which you would graph a two-dimensional relation, such as a line or parabola. All such graphs are flat; they lie in a single plane, or flat surface, which is two-dimensional.
If we add a third axis, a z axis, we will be able to give each point that we plot a height above the paper, as well as horizontal and vertical coordinates. The point (3, 2, 4), for example, represents a point that is located at a distance from the centre that is 3 units right, 2 units up (on the x-y plane), and 4 units above the paper. 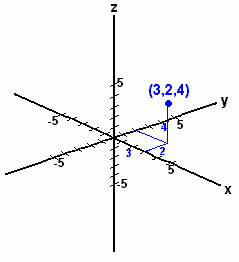 Here is the point (3, 2, 4) on the grid.
Here is the point (3, 2, 4) on the grid.Three-dimensional graphs are difficult to draw on paper, but you should be able to visualize the point as being located 'in space', rather than on a flat surface. (The blue lines are there to help you see 'in 3-D'). 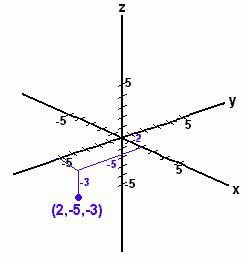 If the centre of the grid represents you, for example, the point (3, 2, 4) might be a fly in the air somewhere in the room. If the centre of the grid represents you, for example, the point (3, 2, 4) might be a fly in the air somewhere in the room.Here's another grid, showing the point (2, -5, -3). This one's a little harder to visualize, because it's under the paper! Now let's look at a pair of points plotted in three-dimensional space, with a line joining them. 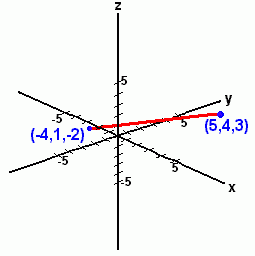 The points are (-4, 1, -2) (below the x-y plane) and (5, 4, 3) (above the x-y plane). The red line joins the points through space; the distance between these points (distance d) is the length of the line segment that joins them. The points are (-4, 1, -2) (below the x-y plane) and (5, 4, 3) (above the x-y plane). The red line joins the points through space; the distance between these points (distance d) is the length of the line segment that joins them. The distance can be calculated using: 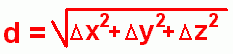 This is just the common distance formula, or Pythagorean Theorem, extended to three dimensions by including the difference in the z coordinates. Let's actually work out the distance: 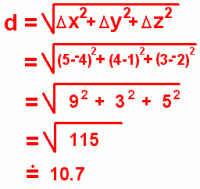
You can see that the formula works just like the two-dimensional version. It gives the distance between any two points in three-dimensional space, as long as you know the coordinates of those points on the grid. |