 and π radians Angles are most often measured in degrees, where the point (0, 0) is the centre of the angle, and the angle is then measured counter-clockwise.  
There is another method to measure angles, a method which is commonly used in trigonometry and physics. It uses radians and π radians. A radian is defined as the angle that results when you divide 180° by π π, or pi, is the value 3.14159 ... [find out more about pi here] 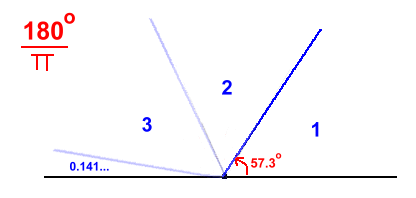 The resulting angle is 57°.29577951..., which, like π, is an irrational number. From the diagram above, you can see that there are just over three radians in 180°. In fact, there are precisely 3.14159..., or π of them. Using this conversion, we can represent angles in π radians: For example, 90°, which is half of 180°, would be π/2 radians, or πr/2, or π/2r Here is a list of the most commonly used angles ...  You'll also see them shown on a diagram ... 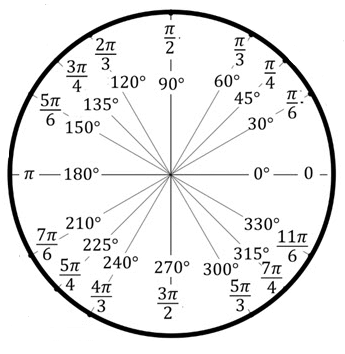
Converting Degrees to π radians Express the angle as a fraction of 180 π radians, and reduce: 120° = 120/180 πr = 2/3 πr 80° = 80/180 πr = 4/9 πr 450° = 450/180 πr = 5/2 πr 17° = 17/180 πr ≈ 0.09 πr Converting π radians to degrees 3/4 π radians = 3/4 (180°) = 135° π/6 radians = 180°/6 = 30° Notice that we're exchanging π radians for 180 degrees. This can lead to some confusion because of the way many textbooks (and teachers) represent π radians, especially when doing trigonometric operations. It is common practice to drop the 'r' representing radians when writing the angle. So instead of cos(π/6r), you will see cos(π/6) When confronted with something like sin(3/2π), you may wonder why you don't replace the π by 3.14159... The reason is, of course, that it's not sin(3/2π), but actually sin(3/2πr), and you're replacing the πr by 180°, since π radians are 180° |