 A prism is a three-dimensional object where the two ends are identical. A rectangular prism is one where the sides and ends are all rectangles. All the prisms we look at in high school math courses are also right ones, where sides meet each other at 90°, so this page is really about right rectangular prisms. For simplicity when you're first learning about them, we'll often just call them rectangular boxes.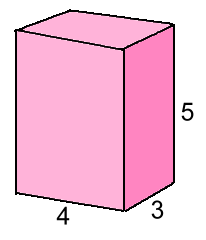 
Here's a box that is 3 cm wide, 4 cm long, and 5 cm tall.We want to find the volume of this prism, which is the number of cubic centimetres it will hold. 
One cubic centimetre (1 cm3)
One way to find the volume would be to show the diagram made up of individual cubic centimetres: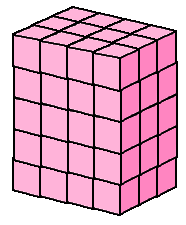  
There are five layers, corresponding to the height h = 5. Each layer is a rectangle, 3 cm wide and 4 long.  Each of these layers has 4 x 3 = 12 cubic centimetres Altogether, the 5 layers contain 4 x 3 x 5 = 60 cm3.
I think you've realized that there's a much quicker method, one that doesn't require that you draw a detailed picture.We can get the volume by multiplying the sides: Volume = Length x Width x Height V = 4 x 3 x 5 V = 60 cm3 This shortcut is a formula:
Here's an example using the formula: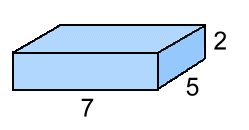 
V = L · W · HV = 7 x 5 x 2 V = 70 cm3 Here's one where you have to find a missing side: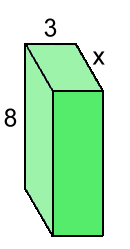 
The volume of this box is 96 cm3.How big is the missing length x? Always start with the formula, and fill in what you know: V = L · W · H 96 = x ·3 · 8 and solve: 96 = x · 24 96/24 = x 4 = x The next example: find side x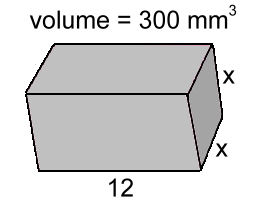 
V = L · W · H300 = 12 · x · x 300 = 12 · x2 300/12 = x2 25 = x2 5 = x by doing a square root The final example: find the volume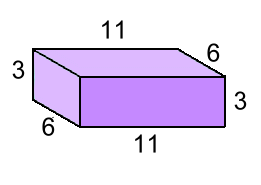 
V = L · W · H V = 6 · 11 · 3 (just one of each) V = 198 cm3 NOTE: You don't need to worry about which is which when you're filling in L, W and H. By standing the shape on its end or on a side, all the names will switch anyway ... a height becomes a length, a width becomes a height, and so on. Just fill in the three numbers in whatever spots you want. |