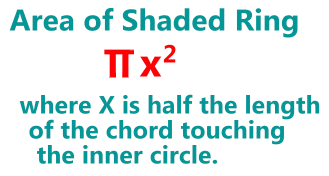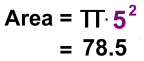A typical ring problem in grade 9 math is to find the shaded area of the ring, as shown on the left. The standard method for solving this, given the radii of the two circles, is to find the area of the entire circle, and then subtract the area of the 'hole', leaving the area that's shaded as the answer. For example, if the large radius is 13 and the small radius is 5, you can work out the two circular areas and subtract them, as shown below. 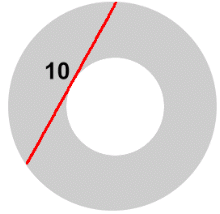Here's a different method to find the shaded ring area: This different method is faster, and is most useful when you know the length of the chord, but don't know the radii. We'll do an example later to show you how easy the formula is to use, but first we'll show that this new formula actually works. Our first step is to determine how long the chord is. We'll use the numbers from the example above. 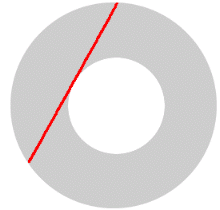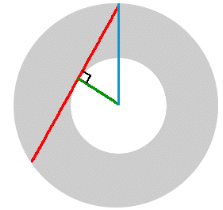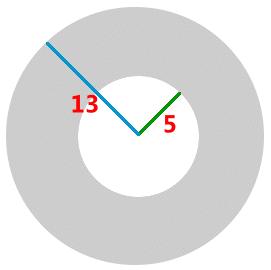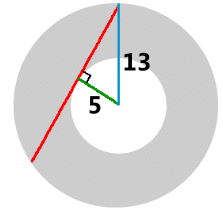Notice that the inner and outer radii placed in just the right spot create a 90° triangle, where we can use the Pythagorean Theorem. 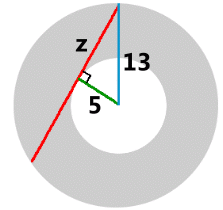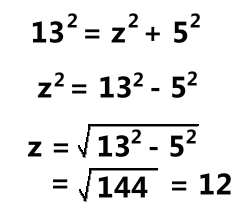The length 12 is exactly half the length of the chord. (This is a theorem from Math 20: "a line from the centre which meets a chord at 90° (the green line) will bisect the chord"). The new rule tells us the area of the shaded ring, using 12 as half the length of the chord: 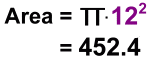... which was the answer we got using the traditional method. Now let's look at how to use this new formula. It is most useful when you know the length of the chord, but don't know the radii. At the left is a shaded ring. We don't know the radii of the two circles, but we do know the length of the chord touching the inner circle ... it's 10. Half of this length is 5, so the area of the shaded ring should be: This rule is a handy carpenter's trick for finding the area of a circular ring. By drawing a chord that just touches the inner edge of the ring, and finding half that length, it's just a quick calculation using Another way to state this new rule: The area of a ring is equal to the area of a circle with a radius half the length of a chord touching the inner ring. 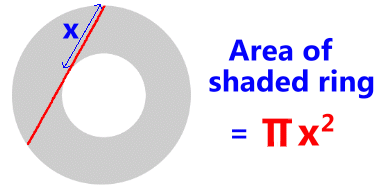Resources