How high can you rip and stack paper? Here are the rules: take an ordinary piece of paper. Rip it in half and stack the pieces ... two of them. Now rip the stack of two, and restack them. You now should have a pile 4 sheets high.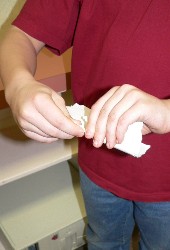



Suppose you keep doing this over and over, ripping the pile in half, each time restacking both parts, and ripping the pile again ...


How high can you make the pile by ripping and stacking?
Enter your guess here. Include units.(eg: 10 cm)



How high do you think the pile would be after just 50 rips?
Enter your guess here. Include units.(eg: 90 cm)



We're going to try this activity to see what happens. We think you'll be surprised by the answers. You can scroll back up later to see how close your guesses were!


We began with one regular piece of paper. First we ripped it in half, to make a stack of two sheets.
Then we ripped that stack in half, to make a new stack four sheets high.


We kept going, ripping and stacking. We began to notice that it was getting harder and harder to rip the stacks.


After ripping and stacking six times, the pile was 64 sheets tall. We couldn't rip this stack ... it was too thick. So we decided to start with thinner paper. We chose the thinnest paper we could find ... a single large sheet of tissue paper ... and started over.


Once again we were stopped after six rips. The seventh rip would have given us a stack 128 sheets high, but the stack was already so thick that we couldn't make a clean rip. If we'd managed it, the next rip would certainly have been impossible.

So far we've answered the first question we asked ... even with very thin paper, you can only rip and stack it, at most, seven times. This would give you a stack just 128 sheets high, or just over one centimeter tall. Not very impressive.

Let's try and answer the second question. If you were strong enough, how high would the stack be after 50 rips? Since it isn't actually possible to do this, we'll have to calculate the answer. We'll make the calculations using ordinary white paper.


We had no way of measuring the thickness of a single sheet of paper directly, so we measured the height of a new stack of 500 sheets.

The stack was 53 mm tall. Dividing this by 500 gives the approximate thickness of a single sheet:  0.106 mm

Now let's find out what happens when we start to rip and stack, beginning with a single sheet.

After:
# of sheets in stack
Height
 
1 rip
2
2 x 0.106 =
0.21 mm
2 rips
4
4 x 0.106 =
0.42 mm
3 rips
8
8 x 0.106 =
0.85 mm
4 rips
16
16 x 0.106 =
1.70 mm
5 rips
32
32 x 0.106 =
3.39 mm
6 rips
64
64 x 0.106 =
6.78 mm
7 rips
128
128 x 0.106 =
13.57 mm = 1.36 cm

This is about as far as you can go when actually ripping, even with tissue paper. What we're going to do, rather than extend the table any more (it's too much work!) is look for a pattern that will let us predict the height after 50 rips.

Here are the first two columns of the table again; notice that the second column is just  powers of 2:

After:
# of sheets in stack
1 rip
2   = 21
2 rips
4   = 22
3 rips
8   = 23
4 rips
16   = 24
5 rips
32   = 25
6 rips
64   = 26
7 rips
128   = 27

In fact, the number of sheets in any stack is "two to the power of the number of rips".
In other words, if you rip and stack 7 times, you're doubling the number of sheets 7 times, or multiplying by 2 seven times, or multiplying by 27.

This makes it easy to work out the number of sheets after 50 rips. Continuing the pattern, it must be 250

How big is 250? Your computer's calculator will give you the answer. It's a stack 1,125,899,906,842,624 sheets high. Since each sheet is only 0.106 mm thick, the stack will be 1,125,899,906,842,624 x 0.106 = 119,345,390,125,318 mm tall .

That's not easy to understand, so we'll convert it to a more useful unit:

119,345,390,125,318 mm = 11,934,539,012,532 cm = 119,345,390,125 m = 119,345,390 km
(divide by 10    ...    then divide by 100    ...    then divide by 1000
Here's the final result:

After ripping and stacking 50 times, the pile will be 119,345,390 kilometres tall!

That's about the same as 2,984 times around the Earth at the equator, or 80% of the way to the Sun from Earth!

Scroll back up to check your second guess. We'll bet you weren't even close!


See another example of exponential growth here.

Math students need be able to recognize the first ten or so powers of 2 from memory. To help you with this, we've listed them on a separate page here that you can print. You might also want to review powers and exponents.

Resources