 On this page we'll show you how to find the arc length a and the area A of the sector. 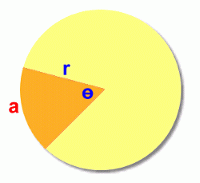 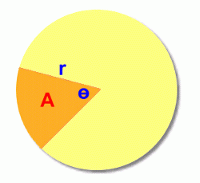 Finding Arc Length 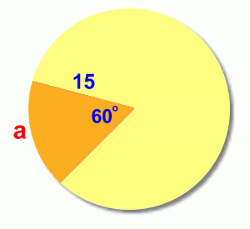
We'll use a circle with radius 15 cm and central angle 60°. The first step is to find out what fraction of the circle is represented by the central angle 60°: 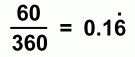 The sector represents 1/6 of the circle, or 0.1666... of the circle. To find the arc length a, we now need to find the circumference (the distance around the full circle), and then find 1/6 of it (multiply it by 0.1666...) 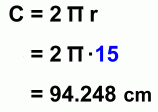
 This is the length of the arc a. This method will work for any sector in any circle. You just need to find the fraction of the circle that the sector angle represents, and then find that fraction of the circumference. Here's a quicker formula to use, summarizing this in one calculation. Math 30 students will learn a new formula for finding arc length: a = r Θ, where Θ is measured in radians. Finding the Sector Area 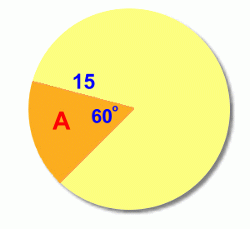
Again we'll use a circle with radius 15 cm and central angle 60°. The first step once again is to find out what fraction of the circle is represented by the central angle 60°: 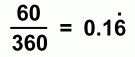 The sector represents 1/6 of the circle, or 0.1666... of the circle. To find the sector area A, we now need to find the area of the full circle, and then find 1/6 of it (multiply it by 0.1666...) 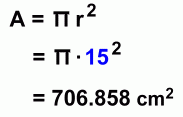
 This is the area of the sector, A. This method will work for any sector in any circle. You just need to find the fraction of the circle that the sector angle represents, and then find that fraction of the area. 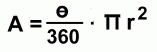 Here's a quicker formula to use, summarizing this in one calculation. |