 Finding a Missing Angle Use the sine law upside down: 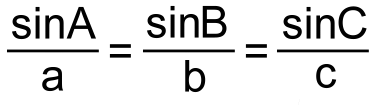 Example 3: Find angle θ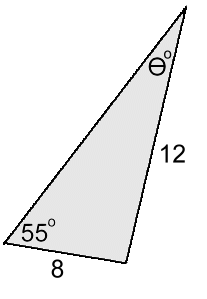 
sinθ sin55 -------- = -------- 8 12 sinθ = 8·sin55 / 12 sinθ = 0.5461 θ = 33° rounded to nearest whole degree Example 4: Find angle θ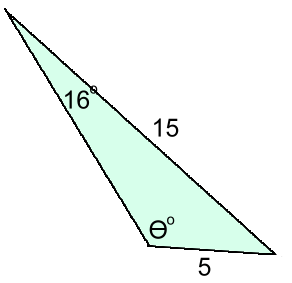 
sinθ sin16 -------- = -------- 15 5 sinθ = 15·sin16 / 5 sinθ = 0.8269 θr = 56° rounded to nearest whole degree Based on the diagram, angle θ must be obtuse, so 56° is actually the reference angle. θ = 180 - 56 = 124° Whether you're finding a missing side or a missing angle, the sine law works for some non-90° triangles, but not all! Have a look at the next example: Example 5: Find side X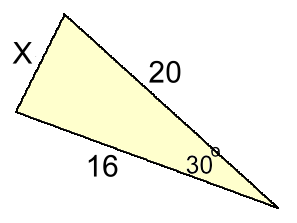 
In order to find a missing side, the sine law requires that you know one other side, the angle opposite that side, and one other angle.
x 20 16 -------- = -------- = -------- sin30 sin?? sin?? We don't have a second angle, so the sine law won't work! The same problem would occur when solving for a missing angle. When this happens, you'll need to use the cosine law. |