|
page six We've shown you that the first of the two numbers you use to break up the root must be perfect. But what happens if you don't pick the biggest possible perfect one? Here's what we mean: There are lots of pairs of numbers that multiply to 200. We want a pair where the first number is perfect. How about 25 and 8? 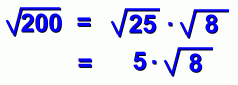 Everything seems to work. But can you see the problem? Our answer can be simplified some more! 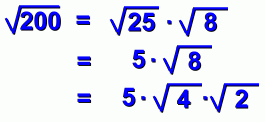 ... and here's the complete solution: 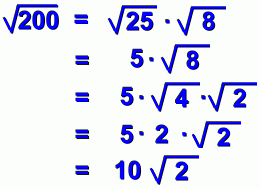 This is the correct answer, but it was a lot of work, mostly because we didn't look for the biggest perfect square that multiplies to 200. In fact, 200 = 100 X 2 as well, and 100 is a bigger perfect square than 25. Moreover, 100 is the biggest possible perfect square that is a factor of 200. Here's the solution the fast way: 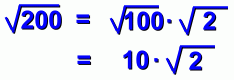 Compare this to the five line solution above. It pays to look for the biggest perfect factor! This is one of the reasons we suggested you memorize some powers, on the 'Powers and Exponents' page, and why teachers in earlier grades insisted you memorize the times tables. Specifically, simplifying square roots is much easier if you have these memorized: 4=2x2 9=3x3 16=4x4 25=5x5 36=6x6 49=7x7 64=8x8 81=9x9 100=10x10 121=11x11 144=12x12 225=15x15 400=20x20 625=25x25 900=30x30 Notice that your calculator isn't much help. If you see the square root of 48, it won't tell you to break it up as 16 x 3! Let's wrap everything up ... |