 An arithmetic series is a sequence which is being added. For example, the sequence 2, 5, 8, ... has a corresponding series 2 + 5 + 8 + ... A series can be added, to give a sum. Here's a typical question: Notice that the series is arithmetic, because there is a common difference of 3. In order to find the sum of 25 terms, or S25, we will need a formula. Here it is:  Let's use this to find the sum S25 for the series 2 + 5 + 8 ..., where a = 2, d = 3, and n = 25 Sn = n/2(2a + (n-1)d) S25 = 25/2(2(2) + (25-1)(3)) S25 = 25/2(4 + (24)(3)) S25 = 12.5(4 + 72) S25 = 12.5(76) S25 = 950 So the sum of the first 25 terms in the series 2 + 5 + 8 ... is 950. Here's a different example. Suppose a certain arithmetic series has first term 5 and last term 47. There are 15 terms in the series. Find the sum of all 15 terms. In this case we know a = 5, and n = 15. But we don't know d. We need a different formula. Here it is: 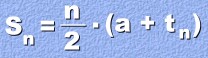 You can use this formula to find the sum of a series when you know the last term (tn). a = 5 tn = 47 n = 15 Sn = n/2(a + tn) S15 = 15/2(5 + 47) S15 = 7.5(52) S15 = 390 The sum of the series 5 + ... + 47, which has 15 terms, is 390. Here's a final example, that's a little different. Let's list what we know: a = 6 d = 2 tn = 44 In order to find the sum of this series, we will have to find out how many terms there are first. Step 1: Find n, the number of terms You already know how to do this, using the term formula, and letting tn be 44: tn = a + (n - 1)d 44 = 6 + (n - 1)2 44 = 6 + 2n - 2 44 = 2n + 4 40 = 2n 20 = n So the series has 20 terms. Step 2: Find the sum. Since we know the last term, we'll use the shorter formula: Sn = n/2(a + tn) S20 = 20/2(6 + 44) S20 = 10(50) S20 = 500 So the sum of the series 6 + 8 + 10 + ... + 44 is 500 |