 A geometric series is a geometric sequence which is being added. For example, the sequence 2, 6, 18, ... has a corresponding series 2 + 6 + 18 + ... A series can be added, to give a sum. Here's a typical question: Notice that the series is geometric, because there is a common ratio of 2. In order to find the sum of 10 terms, or S10, we will need a formula. Here it is: 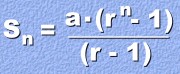 Let's use this to find the sum S10 for the series 4 + 8 + 16 ..., where a = 4, r = 2, and n = 10 Sn = a(rn - 1)/(r - 1) S10 = 4(210 - 1)/(2 - 1) S10 = 4(1024 - 1)/1 S10 = 4(1023) S10 = 4092 So the sum of the first 10 terms in the series 4 + 8 + 16 ... is 4092. Here's a different example. In this case we know a = 72, and n = 9. In order to find r, we'll take a term and divide by the term just before it. Take -24 and divide by 72: -24 ÷ 72 = -1/3 So the value of r is -1/3 a = 72 r = -1/3 n = 9 Sn = a(rn - 1)/(r - 1) S9 = 72((-1/3)9 - 1)/(-1/3 - 1) Using 0.333... for r, and a scientific calculator: S9 = 54.0 The sum of the series 72 - 24 + 8 - ... , which has 9 terms, is 54.0. Here's an example that's a little different. Let's list what we know: a = 1 n = 20 In order to find r, divide 1.1 by 1 ... which gives a value for r of 1.1 a = 1 r = 1.1 n = 20 Sn = a(rn - 1)/(r - 1) S20 = 1((1.1)20 - 1)/(1.1 - 1) Using a scientific calculator: S20 = 57.3 The sum of the series 1 + 1.1 + 1.21 + ... , which has 20 terms, is 57.3. Here's a real problem to illustrate a common use of the sum formula.  A large truck hauling rocks for road construction has to haul its load farther with every trip. Each trip requires twice as much fuel as the previous one. If the truck uses 11 litres of fuel on the first trip, and it makes 6 trips, how much fuel does it use altogether? The first step will be to write the series of numbers that represent the problem, and state what must be worked out. a = 11 r = 2 n = 6 Sn = a(rn - 1)/(r - 1) S6 = 11((2)6 - 1)/(2 - 1) S6 = 11(64 - 1)/(1) S6 = 11(63) S6 = 693 The sum of the 6-term series 11 + 22 + 44 + ... is 693. The truck needs 693 litres of fuel. |