This is a Ferris Wheel ... you've seen one before. This isn't a particularly big one, and it doesn't move very fast, probably because, like all the rides at a street fair, it is designed to fold up and be transported in a truck. Fortunately, it didn't fold up while it was running. At least, while we were watching it. That would have been particularly messy ... Like all machinery that turns in a circle, in order to measure its motion, you have to be able to describe movement in a circle. That's what we're going to show you here. Here's what we saw. The wheel's radius was approximately 7 metres. The wheel turned slowly ... seats moved from one position to the next in about 2 seconds. So the wheel turns through an angle of about  26° in a time of 2 seconds. We could make this our description of turning speed ... 26 degrees in 2 seconds, or 13 degrees per second. There's nothing wrong with that unit, and in fact, some circular motions are measured in degrees per second. But it's often not very convenient; a degree isn't very big, and most machines turn a lot faster than this. Let's try to work out the speed in a unit that's a lot more familiar, in metres per second. How many metres around the outside of the wheel does a seat move in one second? In order to discover this, we'll have to supply some names for the parts of the circle we'll be describing. 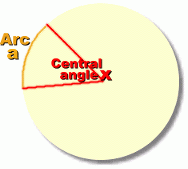The distance the seat moves around the circle in a certain time is an arc of the circle, a. This is a distance we will need to calculate. When it moves this far, the wheel turns through some central angle we'll call x. One complete circle will result when the wheel moves through an angle of 360°, and to do this, the seat will cover one full circumference of the circle. The ratio of the arc length to the full circle is the same as the ratio of the central angle to a full 360°. 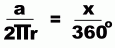We know the radius r is 7 m, and the central angle x is 26°. Pi is of course 3.14. 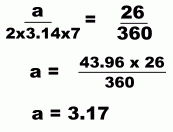This value of a = 3.17 represents the arc of the circle a seat will cover when the wheel turns through 26°. We know this took a time of  2 seconds. So the speed of the edge of the wheel is 3.17 m in 2 seconds, or 1.585 m in 1 second ... or about 1.6 m/s So we can describe the speed of the wheel as 1.6 m/s, around the circle Street Fair Physics