|
that a single drop has less surface area than two smaller drops with the same total volume For simplicity, let's assume that the big drop is split into two identical smaller drops. The volume of the big drop is equal to the total volume of the two small drops. We'll use the fact that these volumes are equal to find out how big the smaller drops are. (The radius of a small drop is not half the radius of the big one, even though the volume is half.) 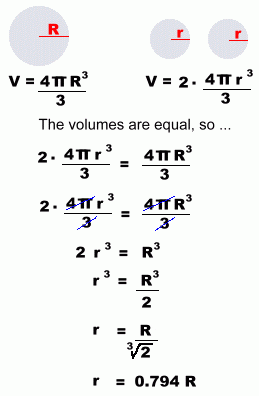 This gives us the result that the radius of a small drop (which has half the volume of the big one) is about 0.794 times the radius of the big drop, or about four-fifths as big. Now we'll use this relation in order to find the total surface area of the two small drops. You'll see that it is less than the surface area of the one big drop.  As you can see, the small drops together have more surface area than one big drop. We can generalize this result as follows: area of the parts is greater than the surface area of the original object." This fact has important consequences in your day-to-day life. Find out more here. |