 Tetration is a notation for incredibly large numbers that I had never heard of before, despite a university degree in mathematics and physics. These were not mentioned anywhere in the popular mathematics books I'd read, including ones by Martin Gardner, who would have been facinated by them. although he did discuss Graham's Number, an extension of this notation, and a number far far greater than a googolplex. I came across tetration on the internet recently, and as always, pretty soon there were all kinds of videos explaining the topic. It's not at all difficult to understand, but many of the pages I came across were unneccessarily obtuse, so I thought I would create a page about them in language that a high school students can understand. Let's start with exponentiation, a notation familiar to high school Math students, and which can lead to some pretty big numbers fairly quickly. Here's an example: 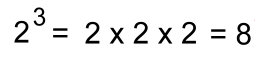 In this power of two, the exponent '3' raised on the right tells you how many 'twos' get multiplied together. With an exponent of just 10, we're already at over 1000: 210 = 1024 Similarly, powers of ten can get very large too. The Earth, for example, has a mass of 6 octillion grams, or 6 x 1024 grams. A googol is 10100. A whole bunch larger! A googolplex is 10googol, or 1010100. Find out more about googols and googolplexes here. Here's a simple example of tetration: Notice that the 'exponent' is on the left! This number raised on the left tells you how many times 2 is repeated as an exponent. 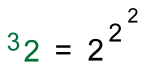 2 is called the base. 3 is called the height of the tetration. 32 is read as the third tetration of 2 These are always evaluated from the top down: 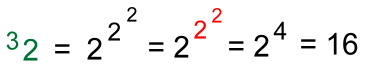
Here's another example, with the height again 3: 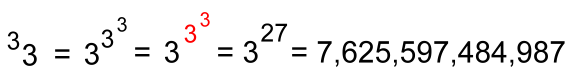
As you can see, these can get very large results with just small bases. Another with height 3: 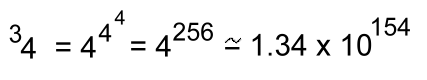 With the base just 4, a tetration with height 3 gives a result that is incredibly large, far bigger than a googol or anything meaningful that we can describe. If we move up to base 10, with height 3: 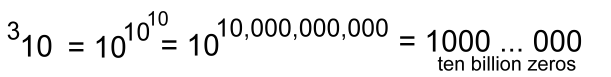 ... another unimaginably large number ... bigger than the total number of atoms in the known universe! Compare this to the exponentiation of base 10: 103 = 1000 Let's try one with height 4, and base 2: 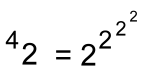 Working from the top down: 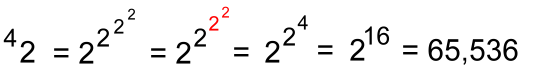
Notice how much larger tetration is compared to exponentiation: Exponentiation: 24 = 16 Tetration: 42 = 65,536 Let's try another one, still with height 4, but with base 3: 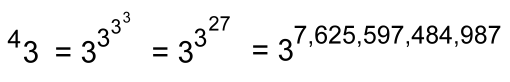
We didn't work this one out because the result is so large that our calculator wouldn't do it! Let's move up a level, back to base 2, but height 5: 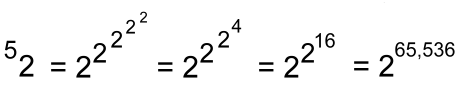 The result, rounded and using scientific notation, is 2 x 10 19,728, once again a number that is so big it defies meaningful description. We'll stop here. This can be continued to get larger and larger numbers, but we've already encountered numbers that have no meaningful referents in the real world. You can see now why tetrations are not discussed in high school or even university math, as they quickly lead to values that are too big to be useful for anything real, even in the realm of astronomy. |