 Example Problem In order to work out problems about how a transformer changes voltage and current, we'll need to develop some equations. Since the voltage is directly proportion to the number of turns, we can write this first equation: 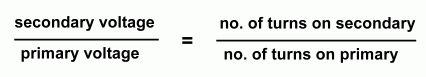 Using symbols, this becomes: 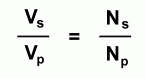 One thing we would like to be able to do is predict the output voltage of a transformer, if we know the primary (input) voltage and the number of turns on both sides. By solving the equation above for Vs, we get: 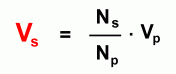 Let's use this to solve a sample problem: "A step-up transformer has 400 turns on its primary coil and 600 turns on its secondary coil. If the primary coil is supplied with 120 V of alternating current, what will be the secondary (output) voltage?"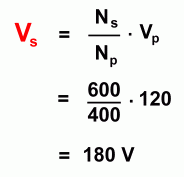 
Using the equation for Vs , and filling in the other values we see that the output voltage is 180 V. "Continuing the problem, suppose the same transformer produces a secondary (output) current of 8 A. What was the primary (input) current?"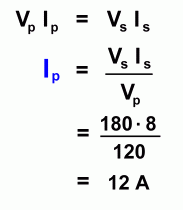 
Since the power (P = VI) is equal on both sides,we get the first equation at the left which can be solved for Ip. Filling in the corresponding values gives an answer of 12 A for the primary current. Notice that this is a step-up transformer. The number of turns on the right is 1.5 times as large as the number on the left. As a result, the voltage went up by a factor of 1.5 (from 120 V to 180 V), and the current was reduced by a factor of 1.5 (from 12 A to 8 A). Another problem: "A transformer with 1000 turns on the primary coil and 500 turns on the secondary coil has a primary (input) current of 40 mA. What will be the secondary (output) current?"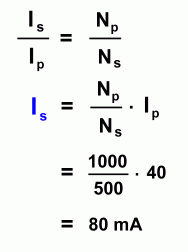 
Because current is inversely proportional to voltage, we get the first equation, relating secondary and primary currents to the primary and secondary number of turns. Solving for Is and filling in the remaining values gives an answer of 80 mA. This was a step-down transformer, which decreases the voltage. But by cutting the number of turns in half, we doubled the current. 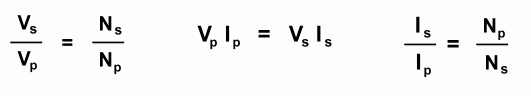 |