First let's identify the sides for a real triangle.
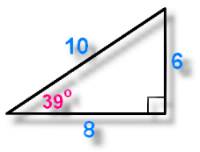Notice where the marked angle 39 degrees is? That makes the names of the sides follow this pattern:
- 6 is the opposite side
- 8 is the adjacent side
- 10 is the hypotenuse
|
Here is another triangle. This time, let's actually work out the three trig fractions you can make from the sides!
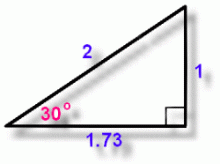Here, 1 is the opposite side, 1.73 is adjacent, and 2 is the hypotenuse.
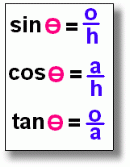
Remembering the word that helps us make the fractions:
..which means:
For this triangle, here are the three fractions you can make:
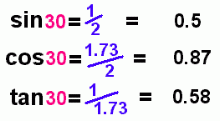
Here's one more example:
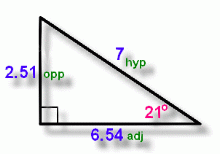This time we've labelled the sides for you. Notice that this triangle is oriented differently, ... but the side names are still determined by where the marked angle 21 degrees is!
So we apply the 'SOHCAHTOA' rule to come up with the three fractions:
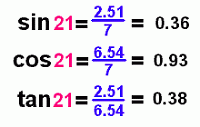
Here's what will make trigonometry so useful. The fractions you get from this right triangle with a 21 degree angle will be the same for every right triangle with a 21 degree angle.
This means that the values of sin 21, cos 21, and tan 21 are always the same, regardless of the size of the triangle! (The sides for a bigger triangle will be proportionally bigger, but the fractions will reduce to the same values).
It also means that your calculator can store the values for these fractions. In fact, it knows the trig fractions for any angle!
Try it out on the example above. Make it work out the sine of 21 degrees.
(You will have to check first that your calculator is actually working with degrees, rather than 'grads' or 'radians'. Change it to degrees if it wasn't there already).
Then enter sin 21, (or 21 sin, if you have an older calculator), and check that you get about 0.36
In your math class, you will learn how to use the trig fractions to solve problems and measure distances.
If you would like to try a quiz based on what we've just shown you, move on to page three.
|