The assignment was to find the height of the gym wall using trigonometry. This kind of calculation can be done by making just three measurements. We'll need the distance to the wall, and the angle of inclination of the top of the wall, and the height of the rotation point on the clinometer above the ground. Then we'll use a trig ratio to help calculate the wall's height.

The first step is to carefully measure the distance to the bottom of the wall from a selected location.
We measured a distance of exactly 10 m to the center point under the tripod.

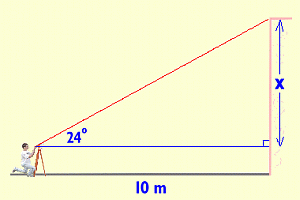
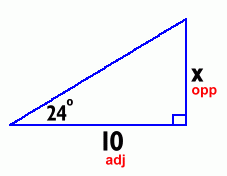
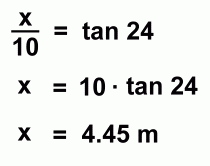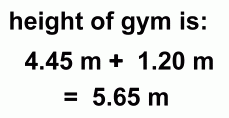The next step is to measure the angle of inclination to the top of the wall. This can be done using a device called a clinometer. We used several different types. A blackboard protractor, thumbtack, string and weight can be used to make a simple one if you don't have a real clinometer.
We did the angle measurement several times, and found an average value of 24 degrees.


Here is our diagram. Our measurements of  24°  and 10 m are shown. When we drew the diagram, we included the height of the clinometer, since the device is actually elevated by the height of the measuring instrument.

We measured that height, and added it to our final answer.
We used two different devices; the calculation we are showing is for the clinometer on a tripod; its height above the ground was 1.20 metres.

Here's the diagram of the triangle we'll be using to solve for  x. The names of the sides are marked on the triangle.

Because we're using opposite and adjacent, the trig ratio needed will be  opposite over adjacent, or  tan.

If you forget the trig ratios, you can recall them using the acronym SOHCAHTOA.

Here is the calculation.

Because all 24° right triangles are similar, the ratios of their sides are always the same. So your calculator can provide the value for what the tan24 ratio is supposed to be.

By rearranging and solving, you can determine the correct value for x to make the side ratio equal to tan24.

Now we need to add on the height of the measuring instrument (and the triangle) above the ground. That value was 1.20 m.

So the height of the gym works out to 5.65 m.

Sr, High Science

How close was our answer? Well, the precision of our measurements could have affected the result. Let's have a look at how precise our values were, and find out what sort of effect this might have had on the calculated result.
The clinometer's scale is labelled in single degrees. Ideally, we should be able to measure an angle accurately to within half a degree. However, the sights on the clinometer are not very good, and there is no telescope to pinpoint the aiming spot 'exactly'. As a result, our angle measurement could have been off by as much as perhaps two degrees.

The measuring tape was more precise, but we didn't make much of an effort to pull it tight. We could have been off on our distance measurement by perhaps as much as 20 cm, or 0.2 m

Lets see what effect this error could have on our answer. Our original measurements were 10m and 24°.

If our measurements were both too big by 0.2m in distance, and 2 degrees of angle, the values might actually have been 10.2m and 26°.
This would make   x = 10.2 · tan26   =   4.97m, and the height of the gym  6.17m
(We will assume, for simplicity, that the error in measuring the height 1.20m of the instrument was negligible)
If our measurements were both too small by 0.2m in distance, and 2 degrees of angle, the values might actually have been 9.8m and 22°.
This would make   x = 9.8 · tan22   =   3.96m, and the height of the gym  5.16m


So we can say that, while we originally calculated the height of the gym to be  5.65 m, its probable height, allowing for errors in measurement, is more likely somewhere between 5.16m and 6.17m.


Resources