 
Page Two Problem 3: 'A communication tower is supported by expensive cables, some of which are attached at the top of the tower. These cables must be attached to the top at an angle of 32 degrees, and at a distance of 80 metres from the base. Calculate the length of one of these cables'. Here is the diagram: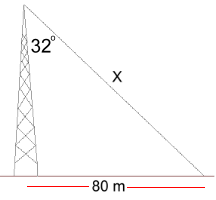 
Here is the diagram with only the essential information, including the side labels: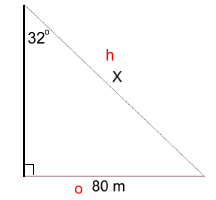 
Here is the solution: 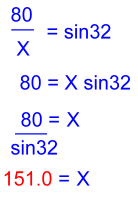Notice that we showed one decimal place, as required. Problem 4: 'A small plane is flying at an altitude of 3.5 kilometres. A person at location A measures the angle of inclination to the plane to be 54 degrees. At the same instant, another person at location B measures the angle of inclination to the plane to be 28 degrees. How far apart are the two people?' Here is the diagram: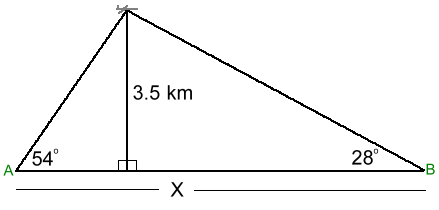 
Here is the diagram with only the essential information. Do you see the problem?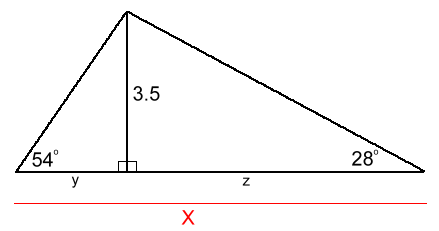 
The distance X we need to find is not the side of a right triangle in the diagram. However, there are two smaller right triangles. If we can find sides y and z, and add these values together, we will get the answer for X.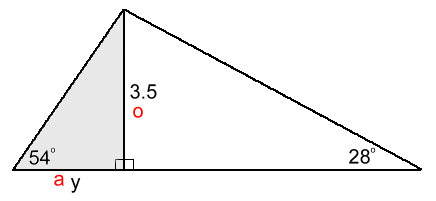 
Let's solve for y in the left triangle first: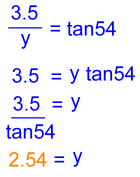
Notice that we're carrying two decimal places in this answer because we're not done yet.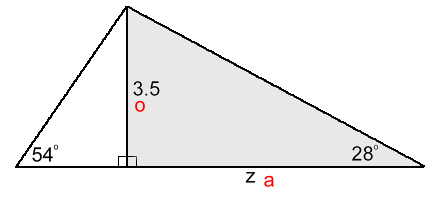 
Now let's solve for z in the right triangle: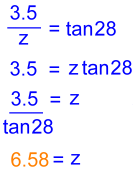
Notice again that we're carrying two decimal places in this answer.  Let's look at more problems on page three ... |