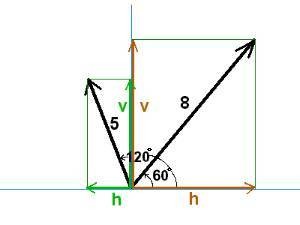
Before we look at how to add two non-perpendicular vectors, you will have to know how to find the components of a vector. The method for adding two vectors involves finding the horizontal and vertical components of each vector, and then adding those components. Have a look at the example below: One vector is 8, at an angle of 60o. The second is 5, at an angle of 120o. The vector 8 has horizontal component h and vertical component v. h = 8 cos60 = 4      v = 8 sin60 = 6.9 The vector 5 has horizontal component h and vertical component v. h = 5 cos120 = -2.5      v = 5 sin120 = 4.3 The horizontal components add to 4 + -2.5 = 1.5 The vertical components add to 6.9 + 4.3 = 11.2 Now make a diagram to show these totals as vectors. 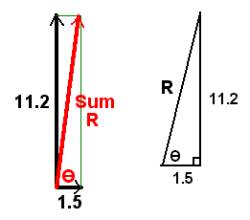One is a horizontal sum, the other vertical: R2 = 11.22 + 1.52 R2 = 127.69 R = 11.3 tan = 11.2/1.5 = 7.47 = 82o The final answer is a vector 11.3 units long, at an angle of 82o There is another method for finding the sum of two non- perpendicular vectors that you will learn in Math 20 (or may have already learned in Math 10), using the sine law and cosine law. This method is easier, but won't be discussed here. Back | Vectors