 
Here's the problem. There is an office building that we'd like to find the height of. We know it's ten stories high, and we have access to the building, including the roof. All equipment needed is available.The goal is to find as many ways as we can to determine the height of the building. We came up with seventeen methods. Here they are, in no particular order. NOTE: The measurements we're using will be chosen for convenience; actual measurements would work exactly the same, regardless of their size. Also, for some of the methods, we can assume that the height of the angle-measuring instrument was taken into account. Method 1: Trigonometry from the ground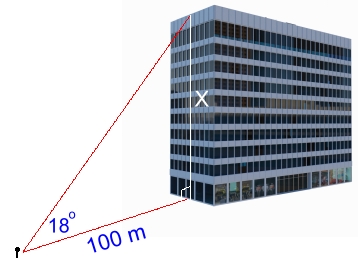 
Standing on the street 100 metres from the base of the building, we measure the angle to the top of the building to be 18°. Using trigonometry:x / 100 = tan18 x = 100·tan18 x ≈ 32.5 m (rounded to 1 dp) Our first method gives an answer of about 32.5 m for the height of the building. Method 2: Drop a Rope From the Roof 
We found a really long rope. From the roof, we lowered it slowly until it just touched the ground.A friend on the ground pulled the rope tight. We marked the rope where it met the top edge of the roof. Our second method gives an answer of 31.4 m for the height. Method 3: Use Trigonometry to Measure the Height Above You of the Top of a Nearby Building of Known Height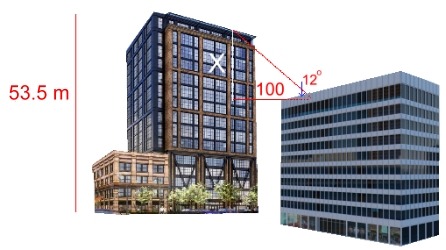 
There is a nearby 15 storey building that you do know the height of. It is 53.5 m tall, its base is exactly 100 m from the base of our building, and we measure an angle of 12° to its top. X will be the height of the other building above us (we're on the roof of our building)X / 100 = tan12° X = 100·tan12° = 21.3 m Subtracting from the height of the building: 53.5 - 21.3 = 32.2 Our third method gives an answer of 32.2 m for the height of our building. Method 4: Find the Building Plans Find out where the city's architectural drawings, engineer's surveys, or building plans are stored. These generally are accessible to the public. Obtain them and find the height. Our fourth method gives an answer of 32 m for the height of our building. Method 5: Use an Altimeter Stand on the roof and measure your altitude using an altimeter. Altimeters measure your height above ground; planes use them, but you can now obtain hand-held versions. There are two types: 
Barometric altimeters (left) use air pressure to measure altitude. They are accurate to within ± 3 m. We used one and got an altitude of 30.2 m.GPS altimeters (right) use GPS satellites to read your height above ground. They are accurate to within ± 2 m. We used one and got an altitude of 33.1 m. Using method 5, we averaged the results to get a buiding height of 31.7 m. Method 6: Contact the Architect We called her and asked her what the height of this building that she designed was. She couldn't remember, but thought it was around 30 m. Our sixth method gives a somewhat dubious answer of 30 m for the height of the building. Method 7: Count the Stories In office buildings, the height of one storey is 4.2 m on average, but this can vary. Using method seven makes our 10 storey building 37.8 metres tall. Method 8: Use a Laser Measurement Tool 
Laser range finders are used for surveying, hunting, as well as in construction. They have an accuracy of within a few millimetres, which for our purposes is negligible.Standing on the roof and holding it upside down, we got a reading of 31.98 m. Our eighth method gives an answer of 31.98 m for the height. Method 9: Find a Building Climber 
Find a person who climbs skyscrapers for fun, and ask him to climb our building with a specially prepared measuring tape in hand. For example, in March 2011, Robert Alain climbed the tallest building in the world, the 828-meter high Burj Khalifa tower in Dubai, taking just over six hours to complete the climb. He, or someone like him, should have no problem with our little building. Our ninth method gives an answer of 35.9 m for the height. We could also use the help of window washers who suspend themselves from ropes from the top of the building. We count that as the same as this method. Method 10: Use the Speed of Sound Have a friend light a large firecracker on the street in front of the building. By peering over the roof's edge with a stopwatch and measuring the time between seeing the explosion (virtually instantaneous, as the speed of light is very fast) and hearing the bang, you could use that time to calculate how far the sound travelled. At a temperature of 20 °C, the speed of sound in air is about 343 m/s. The actual time between seeing and hearing the explosion would be about 0.09 s. Using the equation d = v·t to calculate the distance the sound travelled, we get 30.87 m. However, we wouldn't actually get this result. This method's accuracy is greatly affected by the reaction time of the person using the stopwatch. Having measured stopwatch use previously in a math class, we can confidently say that the reaction time would be about 0.5 seconds. This means that after you see the exploding firecracker, it will be about 0.5 seconds before you press 'start', and another 0.5 seconds after you hear the sound before you press 'stop'. This adds about 1 full second to the time recorded. Given the very short time (0.09 s) measured, this makes our answer meaningless. You can test your own reaction time here. Our tenth method gives no answer for the building's height. Method 11: Use the 'Stick and Shadow' Method History records that in the 6th century B.C., Thales of Miletus measured the height of the great pyramid at Giza by comparing its shadow to the shadow of his staff. We'll use his method to find the height of the building.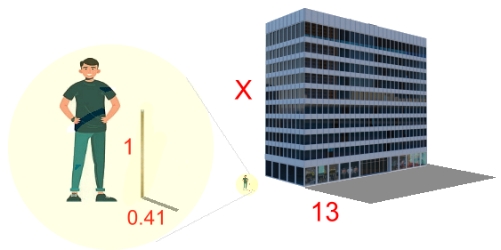 
On a sunny day we recorded the length of a metre stick's shadow. At the same time we measured the length of the building's shadow. The results are shown at the right. Because the angle of the sun is the same for both shadows, we can draw similar triangles ...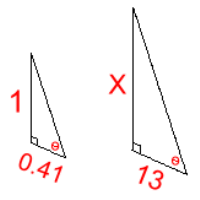 
Making equal ratios: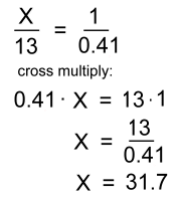
Our eleventh method gives an answer of 31.7 m for the height of the building. Method 12: Use the Pythagorean Theorem Stand on the roof with a fishing rod. With a weight on the end of your line, cast it down to a friend on the street who is 100 in front of the building.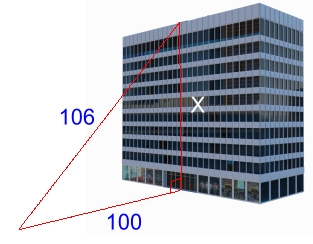 
Pull the line tight and mark it at the reel; wind it in and measure its length. We got 106 m.Solve the right triangle: x2 + 1002 = 1062 x2 = 1062 - 1002 x2 = 1236 x = 35.2 Our twelfth method gives an answer of 35.2 m for the height of the building. Method 13: Weigh Yourself On Top of the Building The farther you are from the centre of the earth, the smaller the force of gravity is on you. This means that on top of the building, being slightly farther from the centre of the earth, you should weigh slightly less. You could use this lesser weight to calculate your height. The formula for the acceleration due to gravity at height h above the surface is: gh = g(1 - 2h/R) where g = 9,81 m/s2, h is your height in metres, and R is the radius of the earth 6.378 x 106 m. We did this calculation. At the top of the building, only about 30 metres above the earth's surface, the force of gravity (your weight) is indeed less. Unfortunately, the difference is so tiny that you would have difficulty finding a scale that could measure it. We found that if you 'weigh' 100 kg at ground level, you would weigh 99.998997 kg on top of the building. You weigh less, but by a practically unmeasureable amount. Yes, we're aware that we're using masses (kg) to represent weights, rather than the actual weights in Newtons. We do this to avoid needless obfuscation for non-physics students. What about at higher heights. What is the force of gravity on the ISS (International Space Station), for example, which orbits the earth at a height of 400 km? It's still about 90% of what it is at the surface of the earth. So if you, at 100 kg, could weigh yourself, you would weigh 90 kg. You can't weigh yourself, of course, because you would be falling ... in orbit around Earth, and technically 'weightless'. Find out more about how weightlessness works here. Our thirteenth method gives no answer for the height of the building. Method 14: Drop Something From the Roof and Time Its Fall 
Stand on the top of the building at the edge, and drop a brick. Use an electronic timer to start as the brick is released. Use a stopwatch to time how long it takes to reach the ground by watching for the brick to explode on the pavement below.Use a formula from grade 11 physics: d = 0.5·g·t2 where d is the distance fallen g is the acceleration due to gravity 9.81 m/s2 You measure the time to be 3.1 s Since your reaction time to press the stopwatch at the end was probably 0.5 seconds, subtract that from the time measured: time = 2.6 s d = 0.5 x 9.81 x 2.62 = 33.2 m Our fourteenth method gives an answer of 33.2 m for the height. Method 15: Time an Echo From the Ground On a quiet Sunday when there is little traffic, stick your over the edge of the roof and yell loudly at the ground below. Wait for the echo to return. Use a stopwatch to record how long that took. At a temperature of 20 °C, the speed of sound in air is about 343 m/s. This method won't work, for the same reason that Method 10 didn't work. The time for the echo to return, even though it's travelling twice the height of the building, is so short that it is smaller than your reaction time when using the stopwatch twice. So any measurement would be meaningless. Our fifteenth method gives no answer for the height of the building. Method 16: Use a Level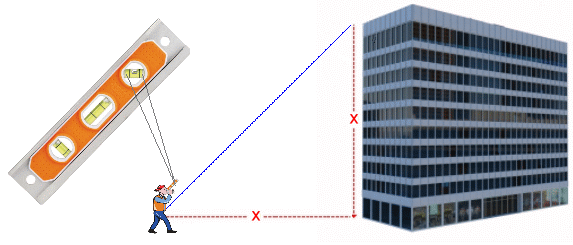 
Position yourself at a spot on the street such that, while sighting along a level at the top of the building, the 45° bubble is centred. This will put you at one of two 45° angles in an isosceles triangle. Measure distance x along the pavement and it will be the same as distance x the height of the building.
Our sixteenth method, remembering to add the height of the level above the ground, gives an answer of 33.7 m for the height of the building. Method 17: Use a Formula for the Distance to the Horizon Long-range rangefinders, called LIDAR devices, can measure distances up to 60 kilometres, with a resolution of 3 m or less. From the top of our building, conveniently at the edge of town, we can see all the way to the horizon.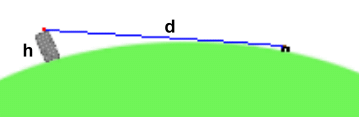 
A friend with a luggage container strapped to the roof of his car drives off, and stops when we can only see the luggage container; the car has just disappeared below the visible horizon. Our LIDAR device pointed at the luggage container gives us a distance to the horizon of 20.81 kilometres.[Aside: the above method directly disproves the ridiculous flat earth notion, since objects will only fall below the horizon on a spherical earth, as anyone living on the seashore knows]. The formula for the visible distance to the horizon d in miles, where h is the height of your eyes above sea level in feet, is given by: 
With a little manipulation, and converting to much more sensible metric units, we wrangled the formula into giving us the height of our eyes h in metres, given the distance to the horizon d in kilometres: 
We measured the distance to the horizon using the LIDAR device and got 20.81 km. Using this in the formula, we obtained a height of 33.99 metres. Subtracting the height of our eyes above the rooftop (1.9 m), we get 32.09 m Our seventeenth method gives an answer of 32.09 m for the height of the building. CONCLUSIONS Even if you're only half awake, you've probably deduced (correctly) that we didn't actually do all of these experiments. We faked it. We used reasonable values for the measurements in each case, and did the math calculations backwards to make sure everything worked. However, the methods that produced answers here would work in real life, even if some of them might be a little difficult to carry out (!) I'm sure there are others methods that would let us find the height of the building. If you have your own idea that you think might work, one that's different than the ones here, and I'll post it with credit to you if it works. No need to include the math; I'll look after that. |