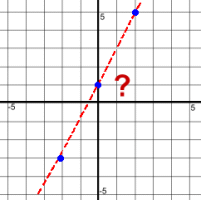
 
Collinear points are three or more points that line up along the same line.Why 'three or more'? This is because two points will always line up. The problem here is to determine if a set of points actually do line up. This can't be done by just looking at the points, because they could be very close to lining up, but actually don't. In order to solve these problems, you'll need to be able to work out slopes.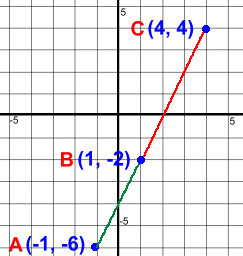 
Let's look at the exmple at the right.There are three points, labelled A, B, and C. Do they line up? If they do, the line segment should have the same steepness, or slope, everywhere along it. In other words, the slope of the green segment should be the same as the slope of the red segment. The line will not bend at point B. Let's work out the slopes of segments AB and BC.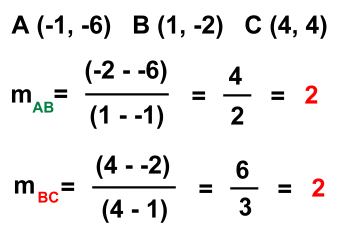 
Because the slopes of each segment are the same, the entire line segment from A to C must form one straight line. We could check by also finding the slope of the entire segment AC, which would also be 2, but that isn't necessary. Our conclusion is that points A, B, and C are collinear. Let's try another example. Have a look at the diagram on the right.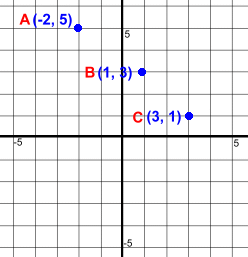 
Are the points A, B and C collinear? Do they line up?Again we find the slopes: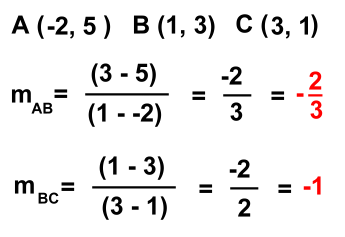 
Because the slopes of the two segments are not the same, the poins are not collinear. Our final example looks at how to find a point that will be collinear with two given points.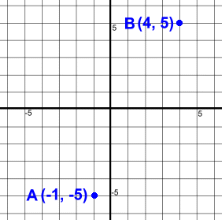 
In the diagram at the right, we know two points:A (-1, -5) and B (4, 5) Of course, these two points are collinear; two points always line up. The problem is to find some other point ... any point we want ... that will be collinear with these two.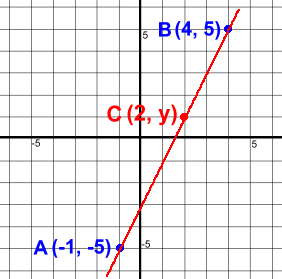 
On the left, you can see that we've shown the line connecting A and B, and picked a point C that looks like it might be on the line (although that wasn't necessary). We picked x = 2, so the point we want will be (2, y) since we don't know its y value. The slope of the whole line: m = (5 - -5)/(4 - -1) = 10/5 = 2 This means that any line segment made with point (2, y) must also have slope 2. We'll use point B: C (2, y) and B (4, 5) must have slope 2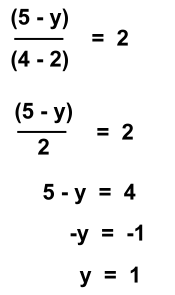 
So the collinear point C = (2, 1). NOTE: We picked an x that looked like it would give a whole number for y, but that wasn't necessary; any x would do. And we still had to do the solving, because the point might have been (2, 1.1), which couldn't have been determined by looking at the graph. You can also find the equation of these lines. |