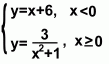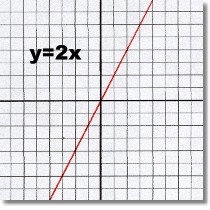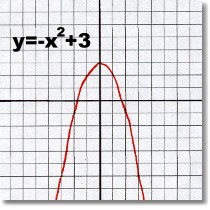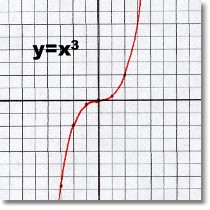
A function is continuous if it has no breaks. On this page we'll first look at some common continuous functions, and then show you the discontinuous ones that you're likely to come across in high school mathematics. Continuous Functions The three functions above are all ones you have seen before: a linear, a quadratic, and a cubic function. The domain of all three is the entire set of Real numbers, and all three functions continue left to right, in both directions, to infinity, without a gap anywhere. 'Continuous' means 'no gaps', or being able to put your finger on the curve and follow it across the grid without having to lift and move your finger. 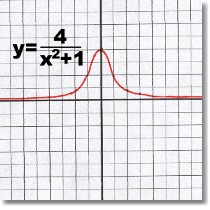On the left above is a function you may not have seen before ... it's asymptotic to the x-axis, and has a maximum y-value of 4. This function is also continuous ... there are no gaps. (Incidentally, notice that despite the x in the denominator, this Rational expression has no undefined values ... the denominator can never equal zero. Can you see why not?) Discontinuous Functions 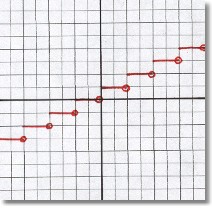This is probably the first discontinuous function you learned about. It's called a step function, and its domain is still the entire set of Real numbers. (The open circles mean that, for example, at x=2, the y-value is no longer 1, but 2). There are clearly gaps when the function jumps to each new value. You can't run your finger along the graph without lifting it to move to the next portion. This function is discontinuous. 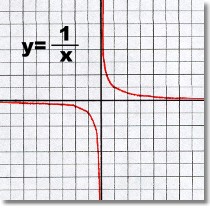The next example, at the right, is a Rational expression function where there is an undefined value of  x. The value of x can never equal zero, since division by zero is not defined. As a result, there is an asymptote at x=0. On either side of this gap the graph approaches infinity. You can't run your finger along the graph without lifting it to move to the next portion. This function is discontinuous. 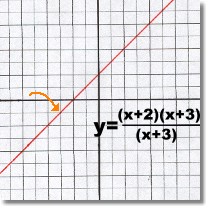The graph on the left is one you may have come across before. It is very mysterious ... the graph all by itself looks like the simple linear function y=x+2. If you examine this function's actual equation, you will notice that it's a Rational expression. The x-value of -3 is undefined. This means there must be a gap at -3, even though you can't see it! The values of x have corresponding points on the graph right up to -3 on either side, but there is no value for x=-3 itself. This one missing point can't be seen, so although there is a gap, it isn't visible! This function is discontinuous. 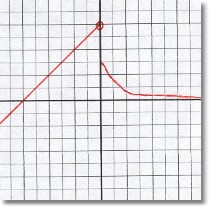There are many types of discontinuous functions, all of which exhibit one common feature; there is always a gap. 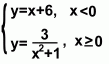At the right is a graph made from two different equations: Again notice that the domain is all Real numbers, but there is still a gap. This function is also discontinuous. Resources Content, HTML, graphics & design by Bill Willis 2023