 How do you find the distance between two points on a graph? This is equivalent to finding the length of a line segment. It's a calculation you will need to be able to do. Let's look at the methods. Horizontally Aligned Points 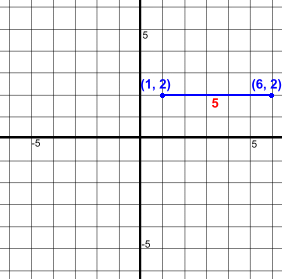 Here are two points (1, 2) and (6, 2)
Here are two points (1, 2) and (6, 2)They are aligned horizontally. It's easy to find the distance between them, or the length of the line joining them, shown in blue. Just count squares. The distance is 5 units. We could also use a simple formula: Δx is the difference between the x coordinates of the points. Δx = 6 - 1 = 5 Let's try another one. 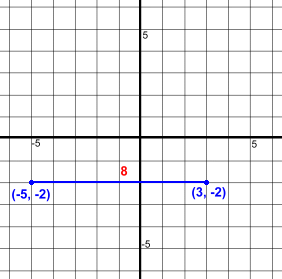 Here are two points (-5, -2) and (3, -2)
Here are two points (-5, -2) and (3, -2)They are aligned horizontally. It's easy to find the distance between them, or the length of the line joining them, shown in blue. Just count squares. The distance is 8 units. Using the formula: Δx is the difference between the x coordinates of the points. Δx = 3 - -5 = 8 The formula may seem unimportant, but we'll need it later. Vertically Aligned Points 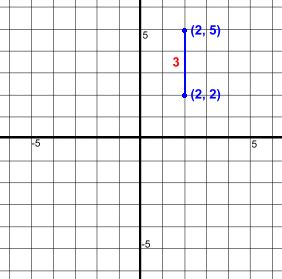 Here are two points (2, 2) and (2, 5)
Here are two points (2, 2) and (2, 5)They are aligned vertically. It's easy to find the distance between them, or the length of the line joining them, shown in blue. Just count squares. The distance is 3 units. We could also use a simple formula: Δy is the difference between the y coordinates of the points. Δy = 5 - 2 = 3 Let's try another one. 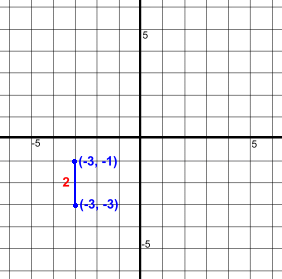 Here are two points (-3, -3) and (-3, -1)
Here are two points (-3, -3) and (-3, -1)They are aligned vertically. It's easy to find the distance between them, or the length of the line joining them, shown in blue. Just count squares. The distance is 2 units. Using the formula: Δy is the difference between the y coordinates of the points. Δy = -3 - -1 = -2 Distances are always positive, so the answer is really 2 Let's use the above example to point out two things:
It's also very easy to imagine points that are aligned horizontally or vertically on a graph mentally, without actually graphing them. Go back to the examples above and see if you can picture them. Obliquely Aligned Points Sometimes points don't line up horizontally or vertically. We'll look at a way to calculate the distance between them, or the length of the line joining them, using the Pythagorean Theorem. Then we'll develop a formula that will be quicker. Move on to page two: Obliquely Aligned Points ... |