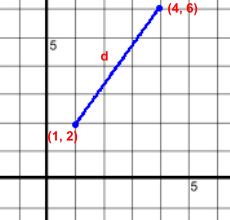
 
For simplicity, we're starting with points joining a line in the first quadrant. All the numbers will be positive.You can't count squares to find distance d when the line segment isn't horizontal or vertical. However, the grid is made from horizontal and vertical lines, so we can construct a right triangle ...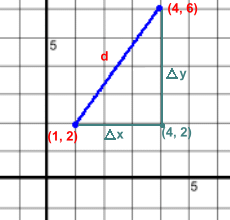 
Here is is. How far is it between (1, 2) and (4, 6)? The sides meet at a right angle, at the point (4, 2) Find the side lengths by counting squares, or using the formulas: Δx = |4 - 1| = |3| = 3 Δy = |6 - 2| = |4| = 4 Now we can use the Pythagorean Theorem: d2 = 32 + 42 = 9 + 16 = 25 d = √(25) = 5 Let's try another one: Find the distance between (0, 1) and (4, 3) 
The sides meet at a right angle, at the point (4, 1)Find the side lengths by counting squares, or using the formulas: Δx = |4 - 0| = |4| = 4 Δy = |3 - 1| = |2| = 2 Now we can use the Pythagorean Theorem: d2 = 42 + 22 = 16 + 4 = 20 d = √(20) = 4.5 (rounded to 1 dp) For an exact value, we leave the √(20), but simplify it: d = √(20) = √(4)·√(5) = 2·√(5) Let's try one where some of the coordinates have negative values: Find the distance between (-3, 3) and (3, -5)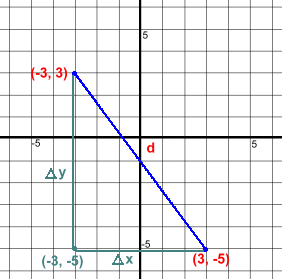 
The sides meet at a right angle, at the point (-3, -5)Find the side lengths by counting squares, or using the formulas: Δx = |3 - -3| = |6| = 6 Δy = |3 - -5| = |8| = 8 Now we can use the Pythagorean Theorem: d2 = 62 + 82 = 36 + 64 = 100 d = √(100) = 10 You may be wondering why we're using the formulas to calculate Δx and Δy. There will be a reason. But first let's do one more example using the Pythagoreaan Theorem. Think about the number of steps necessary: How long is the line segment joining (-4, -3) and (1, 0)?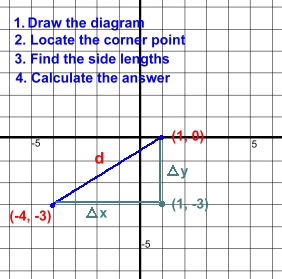 
The sides meet at a right angle, at the point (1, -3) Find the side lengths by counting squares, or using the formulas: Δx = |-4 - 1| = |-5| = 5 Δy = |-3 - 0| = |-3| = 3 (Notice that we subtracted backwards this time) d2 = 52 + 32 = 25 + 9 = 34 d = √(34) = 5.8 (rounded to 1 dp) This method isn't very difficult, but it's a lot of work. Let's look at a much quicker way to find the distance between two points, or the length of a line. Go on to page three for the Distance Formula ... |