 Page Two We need to review static and sliding friction, and Newton's First Law first. Newton described how an object at rest will stay at rest unless a force acts on it. This really means an unbalanced force. In other words, while you sit there in your chair, you are not moving. But there are two forces acting on you ... the force of gravity is pulling you downwards, and the chair is pushing back with the same force. The net result is zero, so there is no net force, and you don't move. Similarly, when an object is moving at constant velocity, there is no net force acting on it. But that doesn't mean there is no force ... just that the forces are equal and opposite. 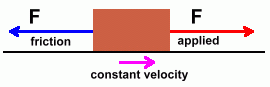 In the diagram above, the object is moving. But it is moving at a constant velocity. There is no acceleration. This is because there is no net force on it. There are two forces acting on the object, both the applied force and the frictional force, but they are equal and opposite, so they cancel each other out. In order to maintain the object's motion at a constant velocity, you must continue to pull with this applied force. The moment you pull less hard, or stop pulling, the frictional force will be stronger and the object will slow or stop. In order to maintain this constant velocity, you will have to pull hard enough to counteract the frictional force, which for a moving object is sliding friction. To get the object moving in the first place, you will have had to apply a slightly larger force, to overcome static friction (which is generally bigger than sliding friction), and to cause some acceleration. But once the object is moving at constant velocity, you only need to pull hard enough to balance the force of sliding friction. If you want to accelerate the object, however, your applied force must be bigger than the frictional force. Here's what happens when you apply a force to an object that is bigger than the frictional force.  That's worth saying again, because it's important. When you apply a force to an object where there is friction, some of the force gets used to overcome the friction. Then, whatever is left can be used to accelerate the object. Let's stick with our 20 kg mass, which weighed 196 N, and look at what happens when we apply a force. 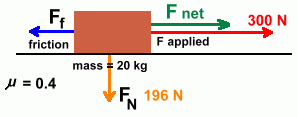
Suppose we apply a force of 300 newtons to the object. The frictional force Ff can be found using: This means that the net force acting on the obect is only 300 - 78.4 = 221.6 N. Now we can find out its acceleration. Using F = m · a, where F is the net force:  What we've just done is to calculate the acceleration on an object by applying a force, where there is friction. In order to do this, we needed to find the frictional force first, and subtract it from the applied force. The remaining net force was used to calculate the acceleration. This type of problem can also be done backwards, where you know the final acceleration, and are required to find out something about the forces. That's what we'll look at next ... go on to page three ... |