Using the Pythagorean Identities .............................

Simplifying

sin²θ + cos²θ = 1
sin²θ = 1 - cos²θ
cos²θ = 1 - sin²θ

tan²θ + 1 = sec²θ
tan²θ = sec²θ - 1
sec²θ - tan²θ = 1

1 + cot²θ = csc²θ
cot²θ = csc²θ - 1
csc²θ - cot²θ = 1

Simplifying Expressions

Example 1:

sinθcos²θ - sinθ

In simplifying these types of expressions, one useful strategy is to factor them.
Here the sinθ is a common factor:

= sinθ(cos²θ - 1)

If you check the list above, you'll find 1 - cos²θ = sin²θ
Switching all the signs, we get
cos²θ - 1 = - sin²θ
Now we can substitute:

= sinθ(cos²θ - 1)
= sinθ(- sin²θ)
= - sin³θ

Example 2: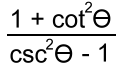

Using two of the Pythagorean identities: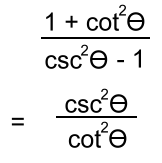

Now we'll change all the trig functions to sin's and cos's: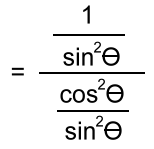

and invert and multiply: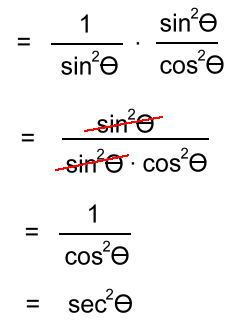

Let's try a few more. Move on to page three ...

Intro | Simplifying | More Simplifying | Verifying

Resources

Content, HTML & design by Bill Willis 2024